Розв’яжіть систему рівнянь
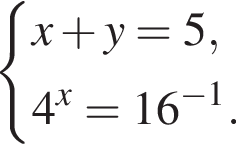
Якщо (x0; y0) — розв’язок цієї системи, то x0 · y0 =
Розв’яжіть систему рівнянь
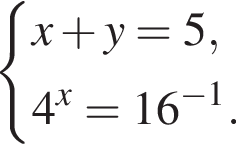
Якщо (x0; y0) — розв’язок цієї системи, то x0 · y0 =
Розв'яжіть систему рівнянь:
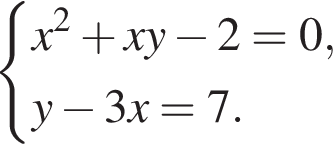
У відповіді вкажіть значення виразу 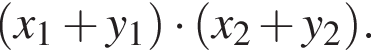
Розв'яжіть систему рівнянь:
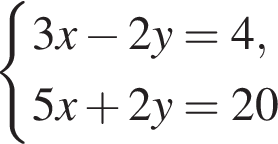
У відповіді вкажіть значення виразу x + 2y.
Розв'яжіть систему рівнянь:
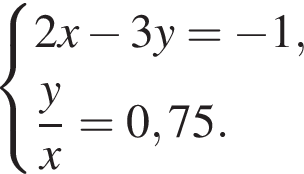
У відповіді вкажіть значення виразу x · y.
Якщо пари (x1; y1) и (x2; y2) — рішення системи рівнянь
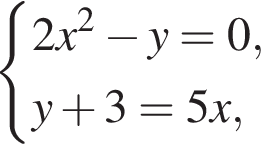
то знайдіть m, де 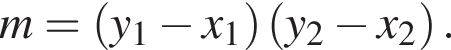
Розв'яжіть систему рівнянь:
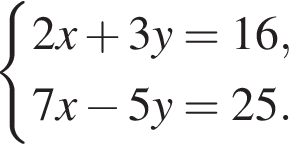
У відповіді вкажіть значення виразу x · y.
Розв'яжіть систему рівнянь:
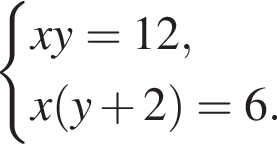
У відповіді вкажіть значення виразу x0 + y0.
Розв’яжіть систему рівнянь
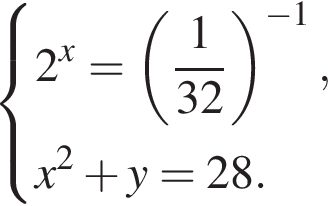
Якщо (x0; y0) — розв’язок цієї системи, то x0 · y0 =
Розв’яжіть систему рівнянь
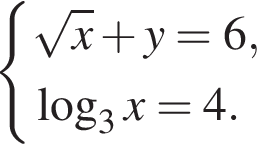
Якщо (x0; y0) — розв’язок цієї системи, то ![]()
Розв’яжіть систему рівнянь
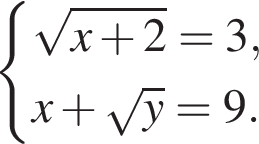
Якщо (x0; y0) — розв’язок цієї системи, то x0 · y0 =
Розв’яжіть систему рівнянь
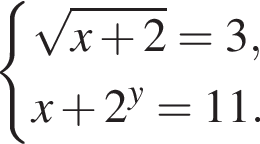
Якщо (x0; y0) — розв’язок цієї системи, то x0 · y0 =
Розв’яжіть систему рівнянь 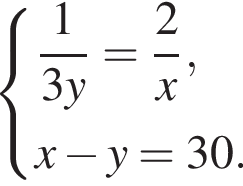 Якщо (x0; y0) — розв'язки рівняння, то чому дорівнює сума x0 + y0?
Якщо (x0; y0) — розв'язки рівняння, то чому дорівнює сума x0 + y0?