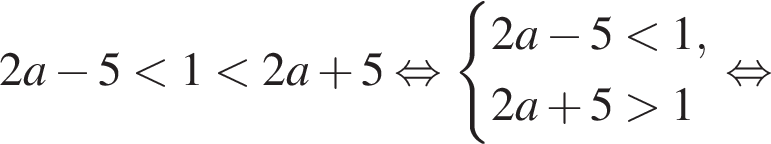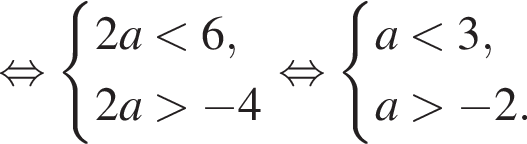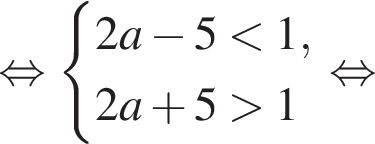У понеділок певний товар надійшов у продаж за ціною 1000 грн. Відповідно до прийнятих у магазині правил ціна товару протягом тижня залишається незмінною, а в перший день кожного наступного тижня знижується на 20% від попередньої ціни. Скільки гривень коштуватиме товар на дванадцятий день після надходження у продаж?
Середнє арифметичне 4 чисел дорівнює 230, одне з чисел дорівнює 80. Чому дорівнює середнє арифметичне інших трьох чисел?
Скільки вершин і ребер у трикутної призми?

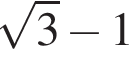
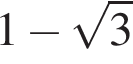
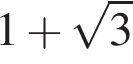
Довжини сторін АВ та ВС прямокутника АВСD відносяться як 2:5, а його периметр дорівнює 28 см. Визначте довжину більшої сторони цього прямокутника.
Розв’яжіть рівняння 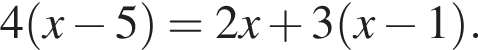
Укажіть з-поміж наведених функцію f(х), якщо для кожного х з області її визначення виконується рівність 
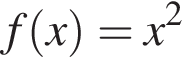
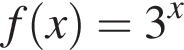
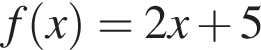

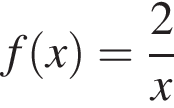
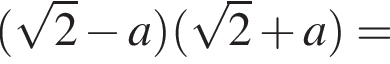
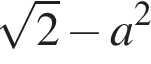
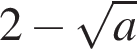
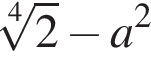
Які з наведених тверджень є правильними?
I. Якщо дуга кола становить 80°, то вписаний кут, що спирається на цю дугу, дорівнює 40°.
II. Якщо радіуси двох кіл дорівнює 5 і 7, а відстань між їх центрами дорівнює 3, то ці кола не мають спільних точок.
III. Якщо радіуси двох кіл дорівнюють 2 і 5, а відстань між їх центрами дорівнює 3, то ці кола торкаються.
Результат спрощення виразу 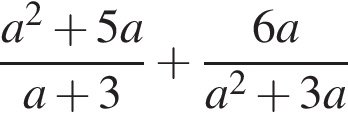 має вид:
має вид:
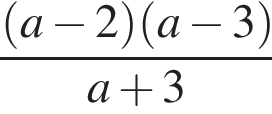
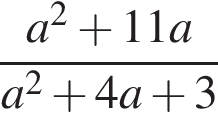
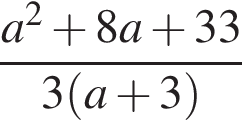
Вкажіть номер малюнка, на якому показано розв’язок системи нерівностей 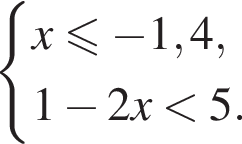
На рисунку зображено прямокутник і рівнобедрений трикутник, які є гранями прямої призми. Довжини основи та бічної сторони трикутника дорівнюють 10 см і 13 см відповідно. Визначте площу повної поверхні призми, якщо площа її найбільшої бічної грані дорівнює 260 см2.
Розв’яжіть рівняння 
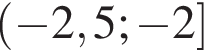
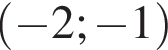
Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Укажіть похідну функції 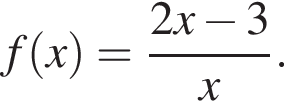
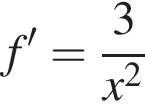
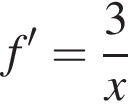
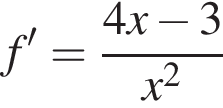
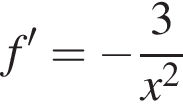
Соотнесите функцию (1−3) и ее свойства (А−Д):
1 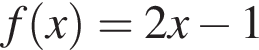
2 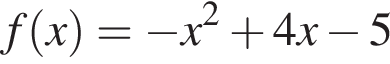
3 
А функция является периодической
Б график функции имеет вид 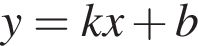
В функция достигает максимума в точке (2; 0)
Г график функции проходит через точку начала координат
Д функция достигает максимума в точке (2; −1)
Установіть відповідність між виразом (1−3) і твердженням про його значення (А−Д), яке є правильним, якщо 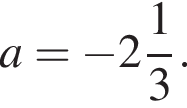
1. ![]()
2. ![]()
3. 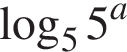
А більше від 5
Б належить проміжку (0; 1)
В є від’ємним числом
Г належить проміжку [1; 5)
Д дорівнює 0
На більшій основі АО рівнобічної трапеції ABCD вибрано точки К та М так, що ВК||CD, MC||AB (див. рисунок). Відрізки ВК та СМ перетинаються в точці О, ВО : ОК = 2 : 3. Периметр чотирикутника ABCM дорівнює 84, ВС = 12. Установіть відповідність між відрізком (1−3) та його довжиною (А−Д).
1. AB
2. MK
3. средня лінія трапецї ABCD
А 21
Б 30
В 18
Г 27
Д 54
В арифметичній прогресії (an) другий член дорівнює 18, а різниця прогресії d = 2,4. Знайдіть суму перших 7 членів прогресії.
Відповідь: ,.
Учні двох класів (у першому — 20 учнів, у другому — 25 учнів) обирають по одному представнику з кожного класу для участі у заході. Знайдіть ймовірність того, що учасниками заходу буде обрано старости цих класів. Вважайте, що всі учні кожного класу мають однакові шанси стати учасниками заходу, і кожен клас має одного старосту.
Відповідь: ,.
В прямоугольной системе координат в пространстве задан вектор 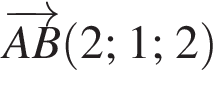 с началом в точке A(−1; −2; 3). Вычислите модуль вектора
с началом в точке A(−1; −2; 3). Вычислите модуль вектора 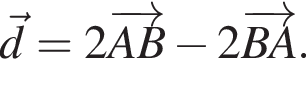
Відповідь: ,.
Визначте кількість цілих значень a, за яких корені x1 та x2 квадратного рівняння 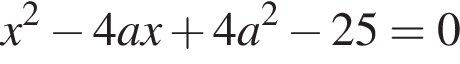 задовольняють умову
задовольняють умову 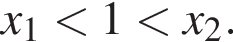
Відповідь: ,.

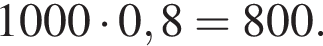
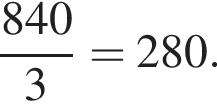
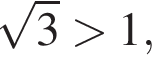 число
число 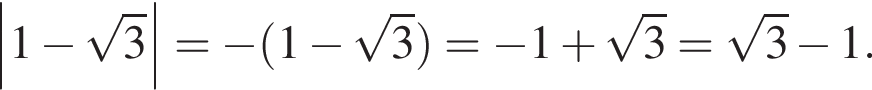
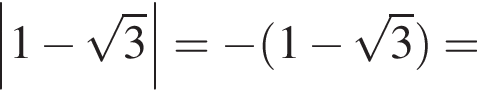
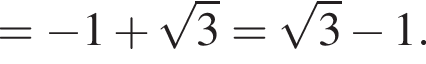
 см
см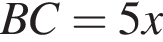 см
см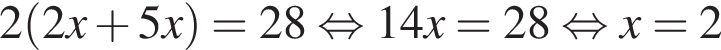 см,
см, см
см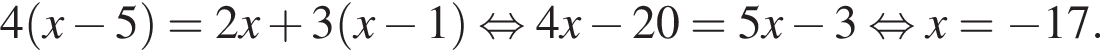
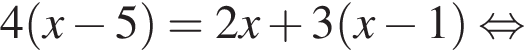
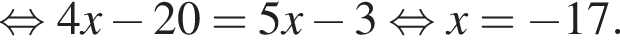

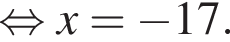
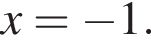 Из этих функций такой будет только последняя. И действительно, при всех x
Из этих функций такой будет только последняя. И действительно, при всех x 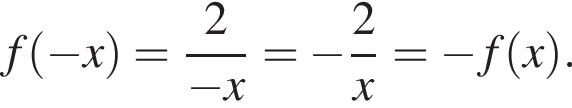
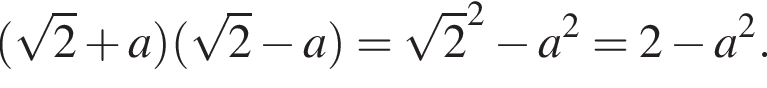
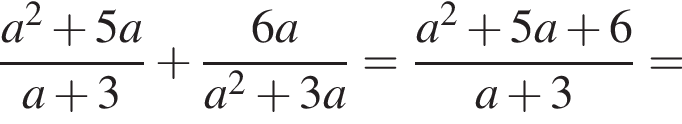
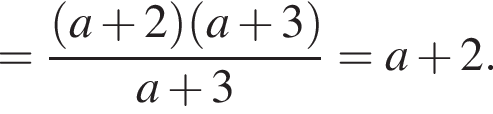
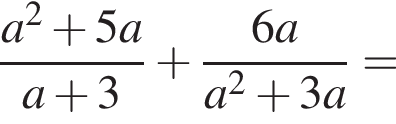
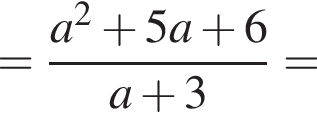
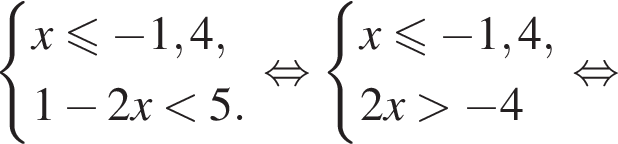
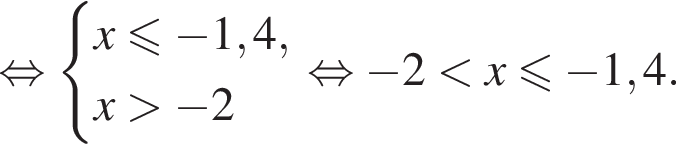
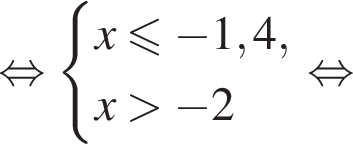
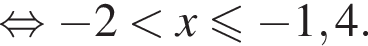
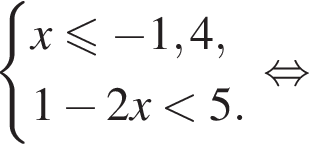
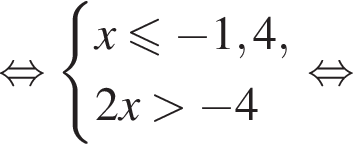
 то есть
то есть 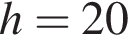 см
см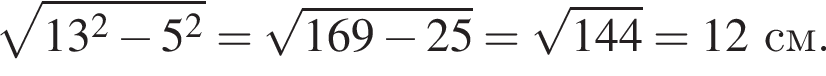

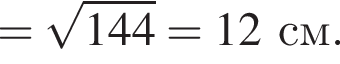






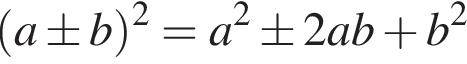 :
: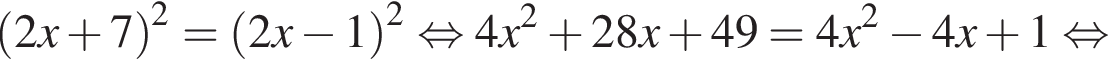
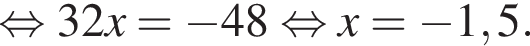
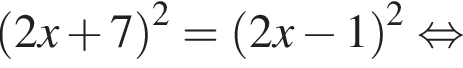
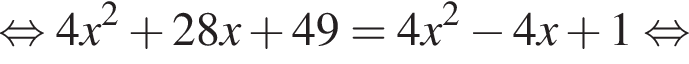
 откуда по теореме Фалеса
откуда по теореме Фалеса  Рассмотрим треугольник ABD MK — средняя линия, следовательно,
Рассмотрим треугольник ABD MK — средняя линия, следовательно, 
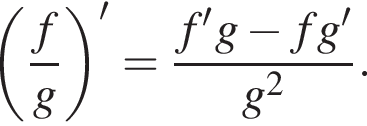
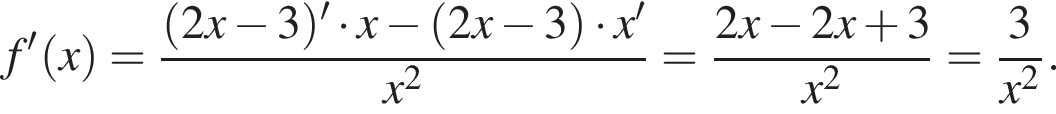
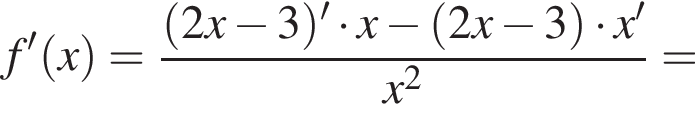
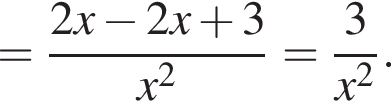

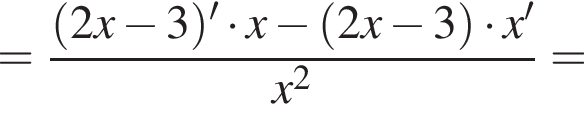
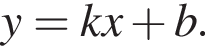 Ответ — Б.
Ответ — Б.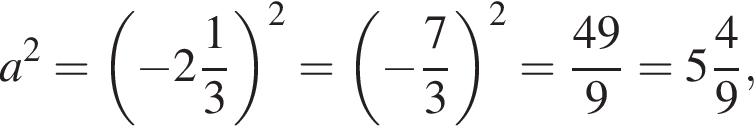
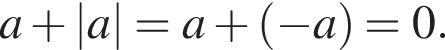 Поскольку
Поскольку 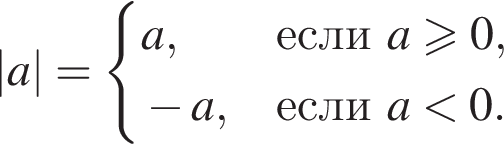
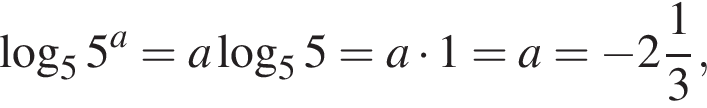
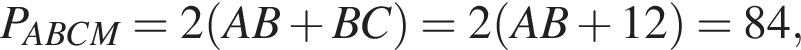
 Прямые AB и CM параллельны по условию, прямые BC и AM параллельны по свойству трапеции. Таким образом, ABCM — параллелограмм. Следовательно, 1 — Б.
Прямые AB и CM параллельны по условию, прямые BC и AM параллельны по свойству трапеции. Таким образом, ABCM — параллелограмм. Следовательно, 1 — Б.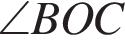 и
и 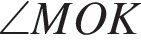 равны как вертикальные углы. Углы
равны как вертикальные углы. Углы  и
и 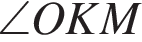 равны как внутренние разносторонние. Тогда:
равны как внутренние разносторонние. Тогда: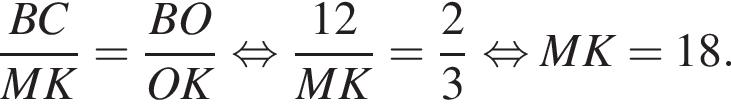

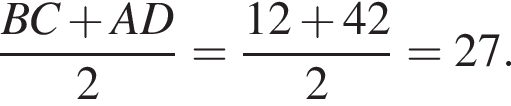
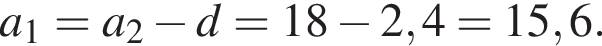 Обчислимо суму перших шести членів арифметичної прогресії:
Обчислимо суму перших шести членів арифметичної прогресії: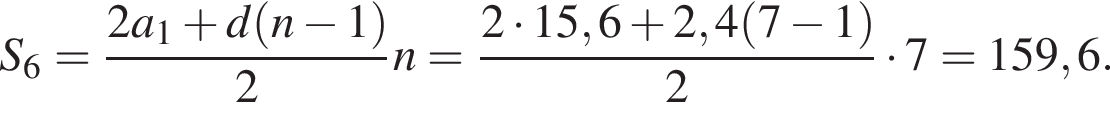
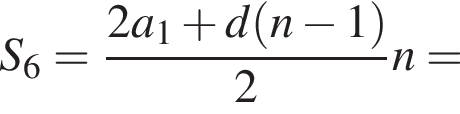
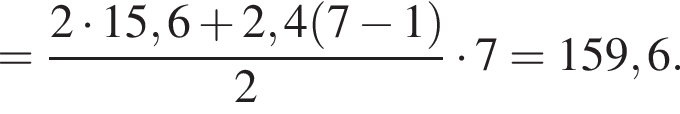
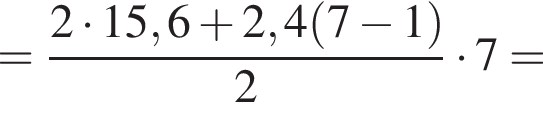

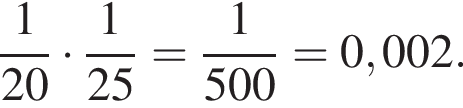
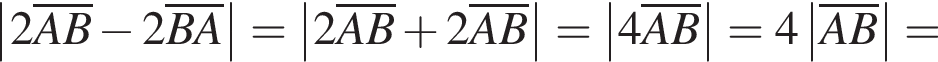
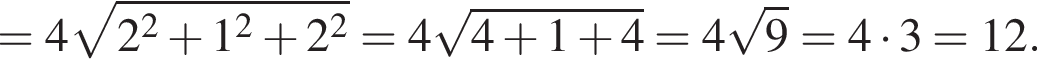
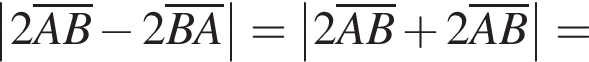
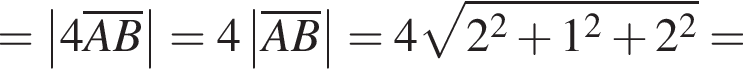
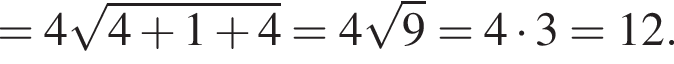

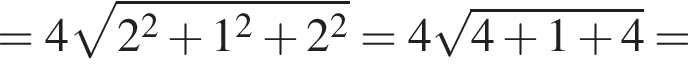
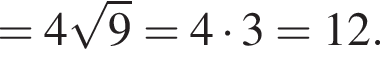
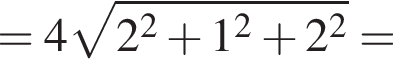
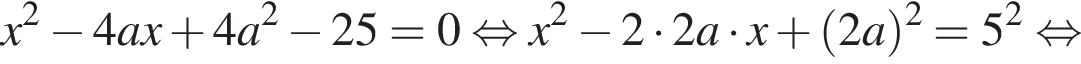
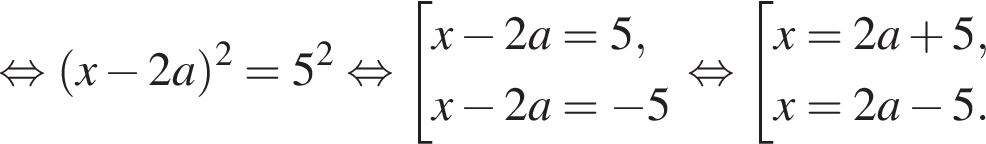
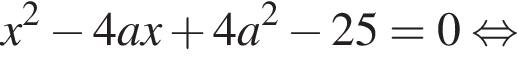

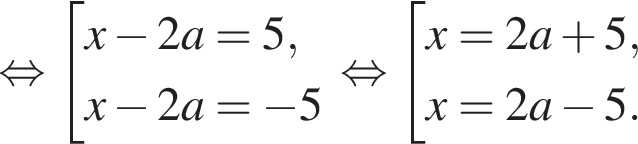
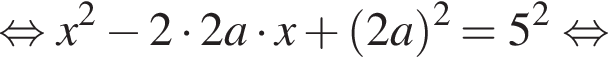
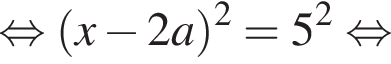
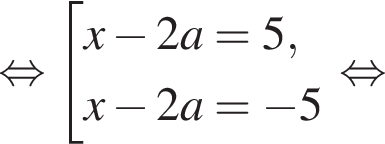
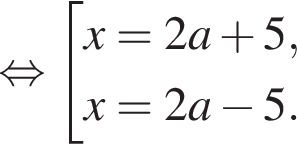
 при всех значениях параметра. Должно быть выполнено условие:
при всех значениях параметра. Должно быть выполнено условие: