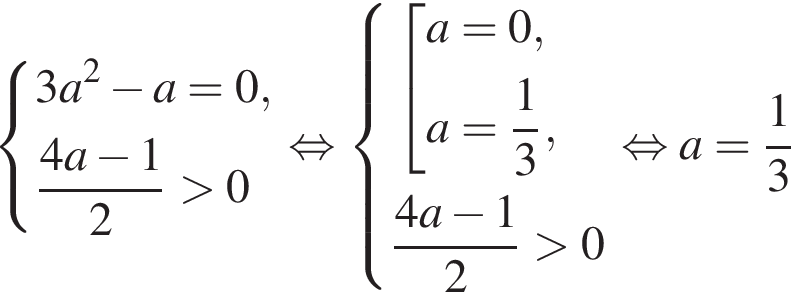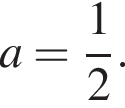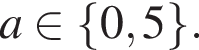Полуниця коштує 180 гривень за кілограм, а виноград – 160 гривень за кілограм. На скільки відсотків полуниця дорожча за виноград?
Після проведення контрольної роботи з математики в одному з класів було отримано такі результати. Знайдіть середній бал за контрольну роботу.
| Оцінки (бал) | 2 | 3 | 4 | 5 |
| Кількість учнів | 8 | 10 | 4 | 2 |
Утворюючий конус є відрізок, що з'єднує
Найдите значение выражения 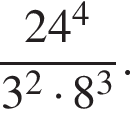
Пряма І перетинає паралельні прямі m та n (див. рисунок). Визначте градусну міру кута α, якщо β = 125°.
Розв’яжіть рівняння 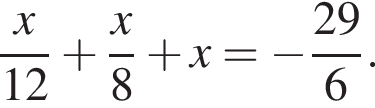
На рисунку зображено графік функції
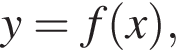 визначеної на проміжку [−2; 4]. Цей графік перетинає вісь y в одній із зазначених точок. Укажіть цю точку.
визначеної на проміжку [−2; 4]. Цей графік перетинає вісь y в одній із зазначених точок. Укажіть цю точку.
Спростіть вираз 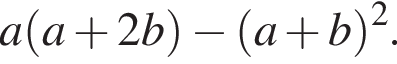
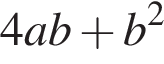
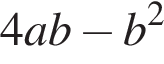
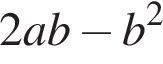
Які з наведених тверджень є правильними?
I. Навколо будь-якого ромба можна описати коло.
II. Діагоналі будь-якого ромба взаємно перпендикулярні.
III. У будь-якому ромбі всі сторони рівні.
Спростiть вираз 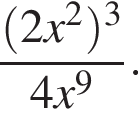
Розв’яжіть систему нерівностей 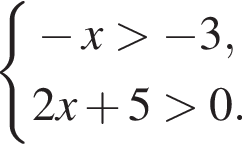
Радіус основи конуса дорівнює 3, висота дорівнює 4. Знайдіть площу повної поверхні конуса, поділену на
![]()
Розв’яжіть рівняння 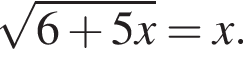
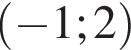
Площа ромба дорівнює 52. Одна з його діагоналей дорівнює 4. Знайдіть іншу діагональ.
Знайдіть похідну функції 
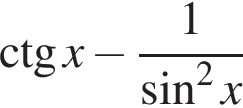

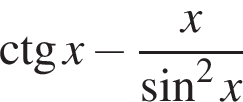
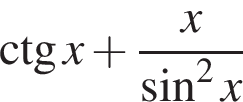
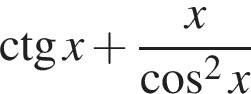
Установіть відповідність між графіком (1−3) функції, визначеної на проміжку [−4; 4], та її властивістю (А−Д).
А функція є непарною
Б найменше значення функції на проміжку [1; 3] дорівнює 2
В функція є парною
Г графік функції не має спільних точок із графіком рівняння 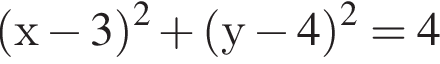
Д графік функції тричі перетинає пряму у = 1
Установіть відповідність між запитанням (1−4) та правильною відповіддю на нього (А−Д).
1. Яке число є квадратом натурального числа?
2. Яке число є простим?
3. Яке число є дільником 8?
А 8
Б 16
В 17
Г 27
Д 56
На рисунках (1−5) наведено інформацію про п’ять паралелограмів. До кожного початку речення (1−3) доберіть його закінчення (А−Д) так, щоб утворилося правильне твердження.
1. Паралелограм, діагоналі якого перетинаються А під прямим кутом, зображено на
2. Паралелограм, менший кут якого дорівнює 30°, зображено на
3. Паралелограм, площа якого дорівнює 16, зображено на
А рис. 1.
Б рис. 2.
В рис. 3.
Г рис. 4.
Д рис. 5.
Рихарду необходимо разобрать 315 квадратных уравнений. Ежедневно он разбирает на одно и то же количество уравнений больше по сравнению с предыдущем днем. Известно, что за первый день Рихард разобрал 11 квадратных уравнений, а справился со всеми он за 9 дней. Сколько уравнений Рихард разберет в последний день?
Відповідь: ,.
У магазині в наявності є 10 видів тортів та 15 видів пачок печива. Скільки всього є способів вибору в цьому магазині або одного торта, або трьох різних пачок печива для святкового вечора?
Відповідь: ,.
У прямокутній системі координат у просторі задано вектор 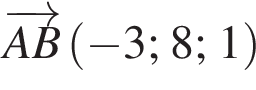 і точку
і точку 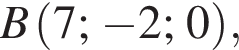 точка О — початок координат. Обчисліть скалярний добуток
точка О — початок координат. Обчисліть скалярний добуток 
Відповідь: ,.
Определите, при каких значениях параметра a, 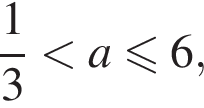 такие, что уравнение
такие, что уравнение 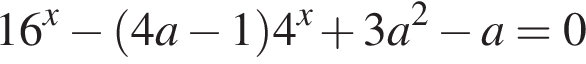 имеет ровно один корень.
имеет ровно один корень.
Відповідь: ,.

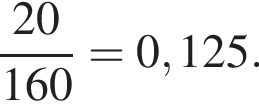
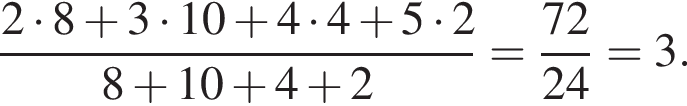
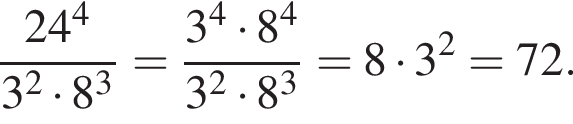
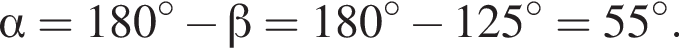
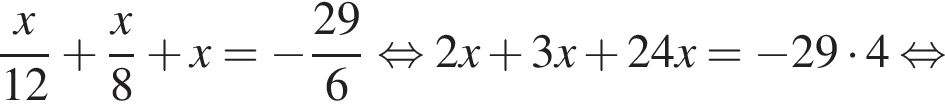
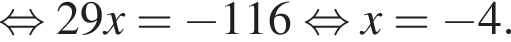
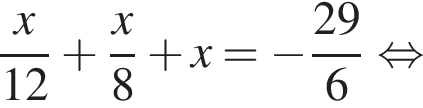
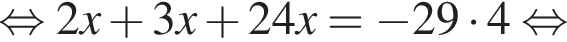
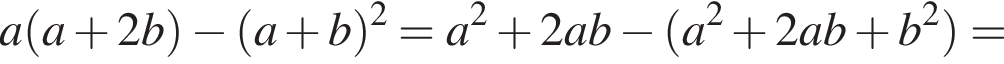
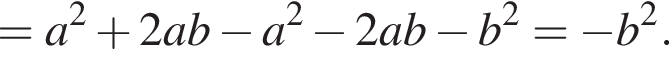
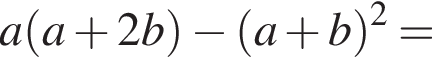
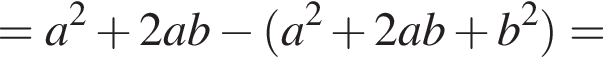
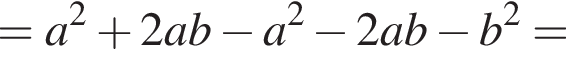
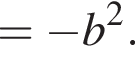
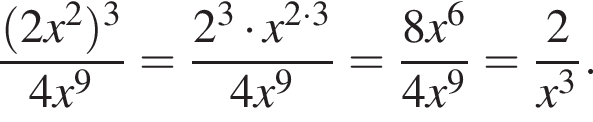
 Значит, ответом будет промежуток
Значит, ответом будет промежуток 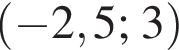
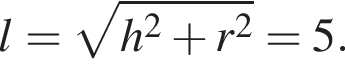 Площадь полной поверхности конуса
Площадь полной поверхности конуса 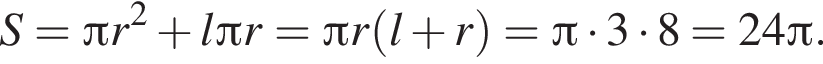
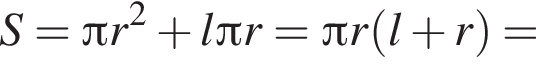
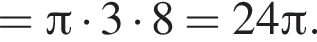
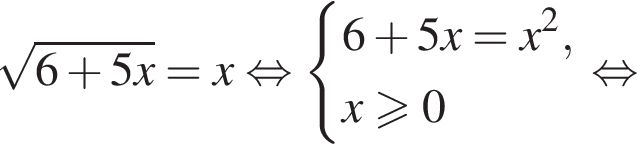
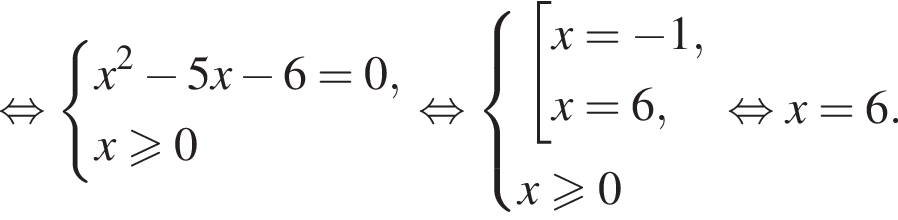
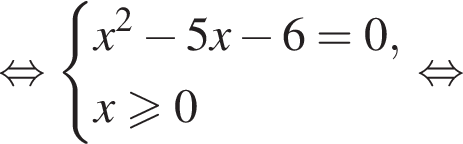
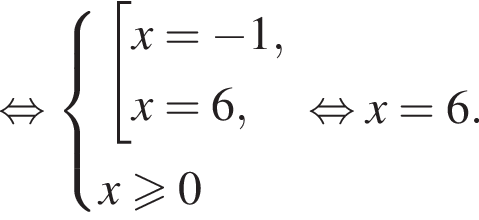
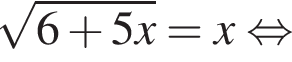
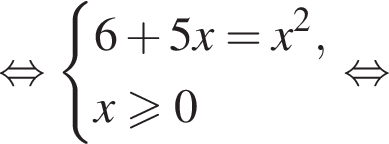
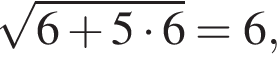 поэтому число 6 является корнем. Подставляя число −1, получаем неверное равенство
поэтому число 6 является корнем. Подставляя число −1, получаем неверное равенство 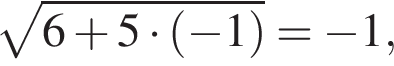 поэтому число −1 не является корнем.
поэтому число −1 не является корнем.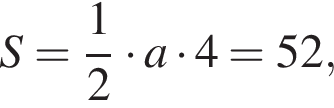
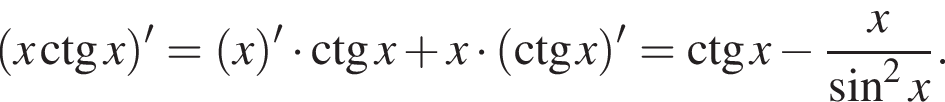

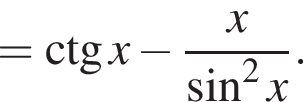


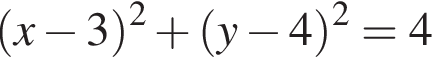 задает окружность, центр которой имеет координаты (3; 4), следовательно, длина радиуса данной окружности равна 2. График данной нам функции не имеет общих точек с окружностью. Таким образом, 1 — Г.
задает окружность, центр которой имеет координаты (3; 4), следовательно, длина радиуса данной окружности равна 2. График данной нам функции не имеет общих точек с окружностью. Таким образом, 1 — Г. Правильный ответ — Б.
Правильный ответ — Б. 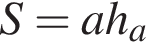 , где
, где  Вычислим площадь параллелограмма:
Вычислим площадь параллелограмма: 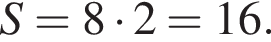 Итак, 3 — Д.
Итак, 3 — Д.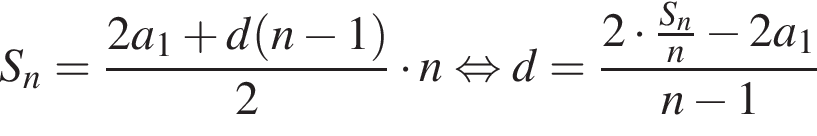
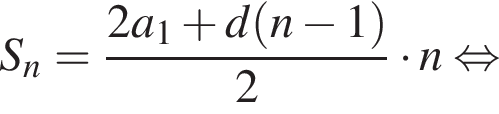
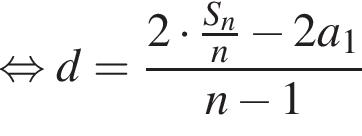
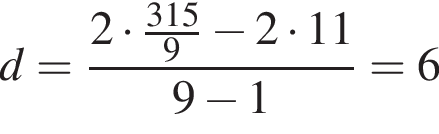 задач.
задач.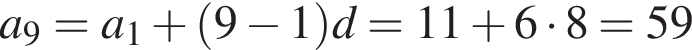 задач.
задач.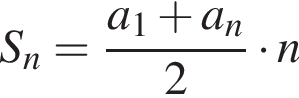 найдем an:
найдем an: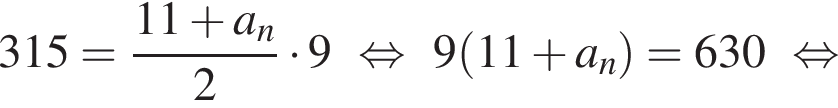
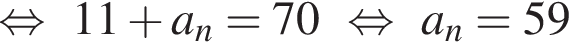
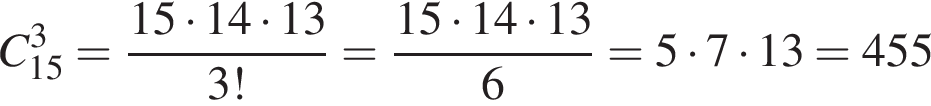
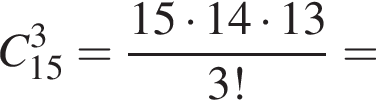
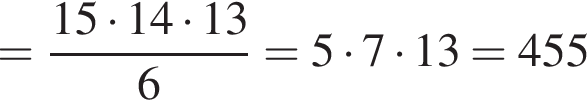
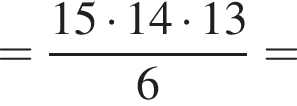
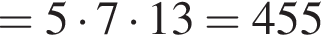
 вариантов.
вариантов.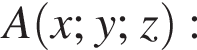
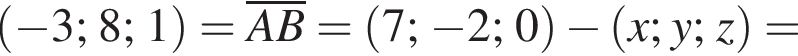
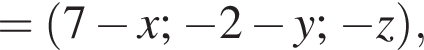
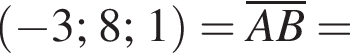
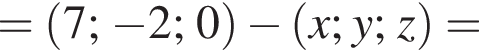
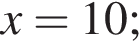
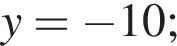
 Найдем скалярное произведение векторов:
Найдем скалярное произведение векторов: 
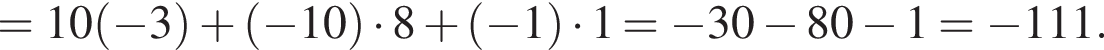

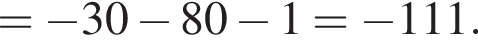
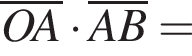
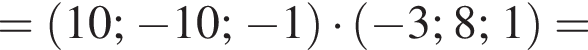
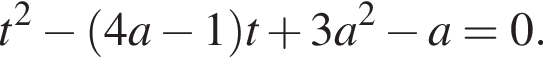 Чтобы исходное уравнение имело ровно один корень, полученное уравнение должно иметь:
Чтобы исходное уравнение имело ровно один корень, полученное уравнение должно иметь:
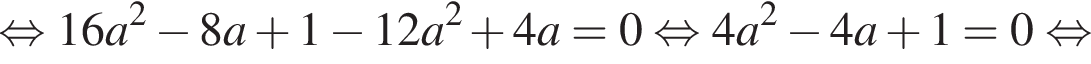
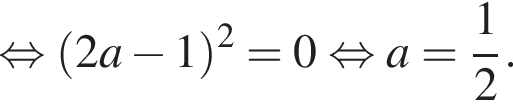
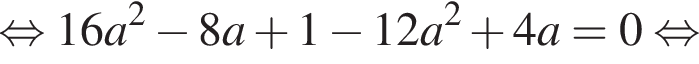
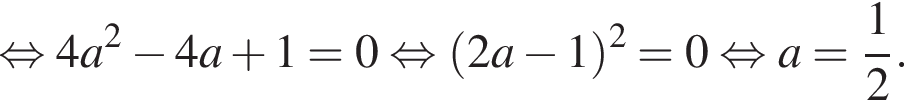
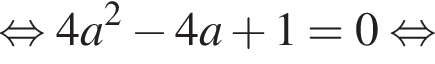
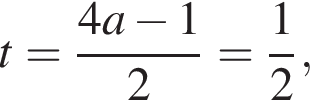 что соответствует условию положительности корня.
что соответствует условию положительности корня.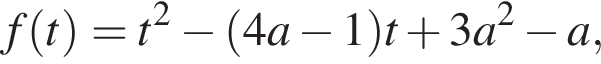 тогда
тогда 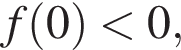 т. е.
т. е. 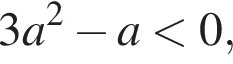 откуда
откуда 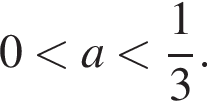
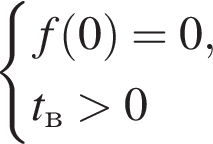 откуда
откуда