На молочному заводі пакети молока упаковуються по 12 штук у коробку, причому у кожній коробці всі пакети однакові. У партії молока, що відправляється в магазин «Куточок», коробок із півторалітровими пакетами молока втричі менше, ніж коробок із літровими пакетами. Скільки літрів молока в цій партії, якщо коробка з літровими пакетами молока 45?
Зростання футболістів, які грали на полі, було 1,74 м, 1,83 м, 1,9 м, 1,81 м, 1,75 м та 2,01 м. Обчисліть середнє зростання футболістів. Відповідь округліть до сотих.
Яка постать є перерізом сфери площиною?
Найдите значение выражения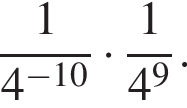 
На малюнку зображені розгорнутий кут AOM та промені OB та OC. Відомо, що ∠ AOC = 102 °, ∠ BOM = 128 °. Знайдіть величину кута BOC.
Знайдіть корінь рівняння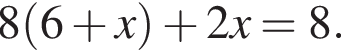
На рисунку зображено графік функції
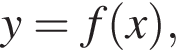яка визначена на відрізку [−4; 3]. Укажіть область значень цієї функції.
Спростіть вираз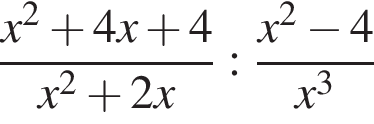 
.
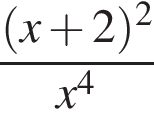
Які з наведених тверджень є правильними?
I. Якщо два кути одного трикутника дорівнюють двом кутам іншого трикутника, то такі трикутники подібні.
II. Якщо два кути трикутника рівні, то рівні також протилежні їм сторони.
III. Якщо діагоналі ромба дорівнюють 3 і 4, то його площа дорівнює 6.
Результат розкладання многочлена x (6 a − b ) + b − 6 a на множники має вигляд:
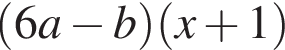
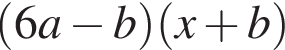
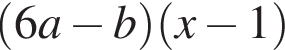
Розв’яжіть систему нерівностей: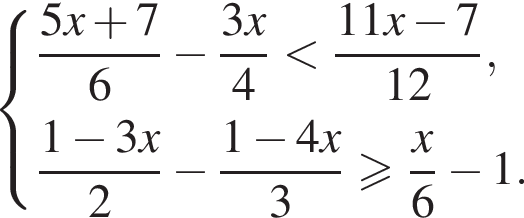 
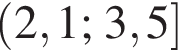
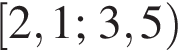
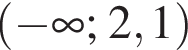
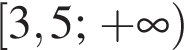
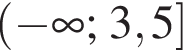
Знайдіть бічне ребро правильної чотирикутної призми, якщо сторона її основи дорівнює 20, а площа поверхні дорівнює 1760.
Розв’яжіть рівняння 
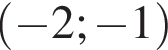
Довжина сторони ромба дорівнює 12 см. Визначте довжину більшої діагоналі цього ромба, якщо його тупий кут
см
см
смВикористовуючи формулу Ньютона-Лейбніца, обчисліть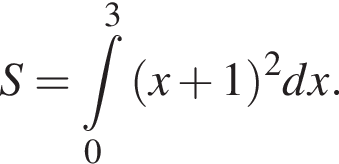 
Увідповідніть функцію (1–3) та її властивість (А–Д).
1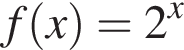 
2 
3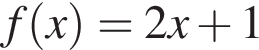 
А функція непарна
Б областю значень функції є множина 
В областю визначення функції є проміжок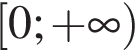 
Г функція спадає на проміжку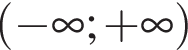 
Д графік функції має лише дві точки перетину з осями координат
Установіть відповідність між твердженням про дріб (1−4) та дробом (А−Д), для якого це твердження є правильним.
1. є скоротним
2. є неправильним
3. є оберненим до дробу 
А 
Б 
В 
Г 
Д 
У прямокутник ABCD вписано рівнобедрений трикутник AKD так, як показано на рисунку. АD = 12 см, АК = 10 см. До кожного початку речення (1−3) доберіть його закінчення (А−Д) так, щоб утворилося правильне твердження.
1. Довжина сторони АВ дорівнює
2. Радіус кола, описаного навколо прямокутника АВСD, дорівнює
3. Довжина середньої лінії трапеції АВКD дорівнює
А 
см
Б 8 см
В 9 см
Г 
см
Д 4 см
Які з наведених тверджень є правильними?
I.Чи вірно, що прямі a і b перетинаються, якщо кожна з цих прямих перетинається з прямою с?
II. Чи вірно, що прямі a та b перетинаються, якщо пряма b перетинається з прямою c, а пряма c перетинається з прямою a?
III. Чи вірно, що прямі a та b перетинаються, якщо пряма a перетинає площину, паралельну до прямої b?
Блок реклами складається з 4 рекламних роликів: про шкоду куріння, про шкоду наркотиків, про шкоду алкоголю та велосипедне місто. Ролик про велосипедне місто заплановано показати двічі — першим та останнім, а решта трьох роликів — по одному разу. Скільки всього існує варіантів формування цього блоку реклами за вказаним порядком рекламних роликів?
Відповідь: ,.
В прямоугольной системе координат в пространстве заданы векторы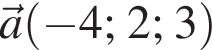 
и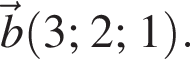 
Обчисліть скалярний добуток 
Відповідь: ,.
Определите наибольшее целое значение a, при котором уравнения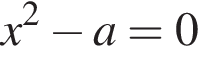 
и 
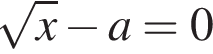равносильны.
Відповідь: ,.
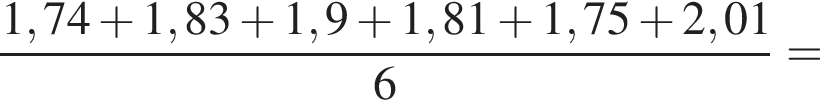
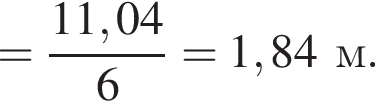
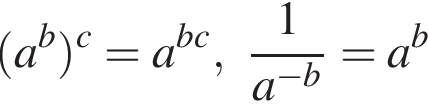и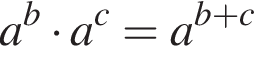 
получаем: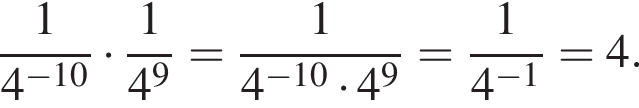
, 
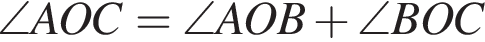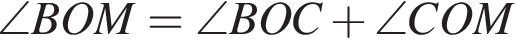и 
. Таким образом:
.
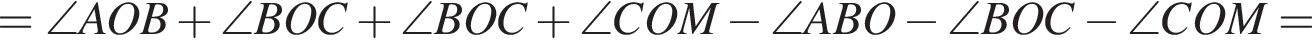
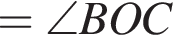
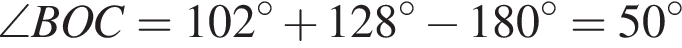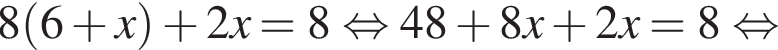
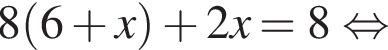
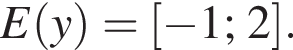
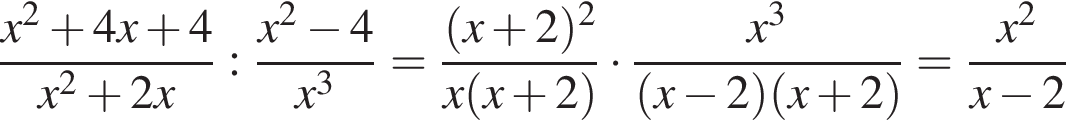
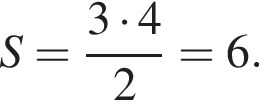
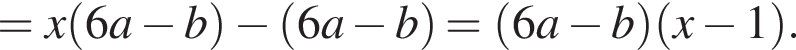
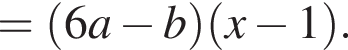
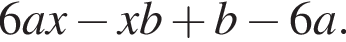
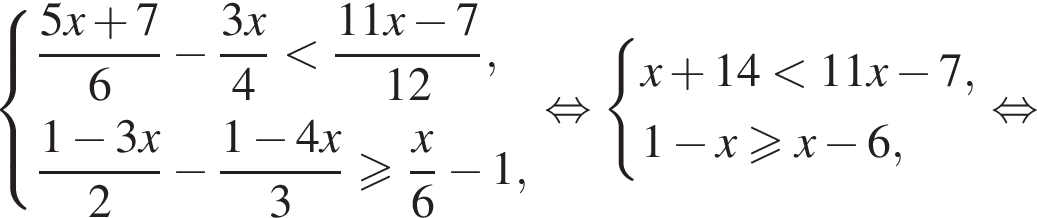
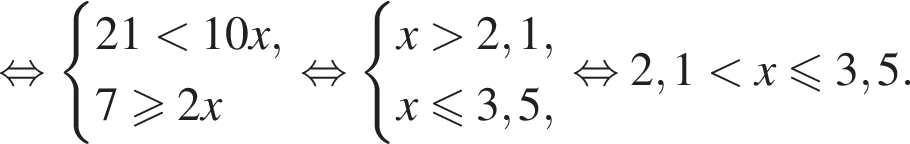
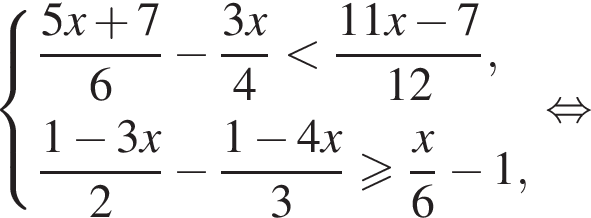
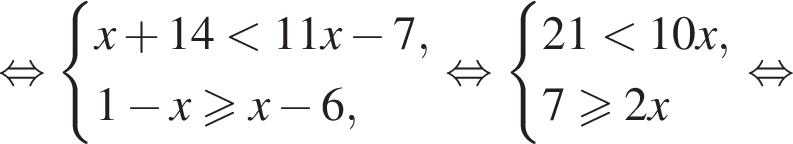
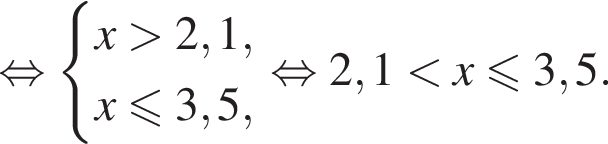
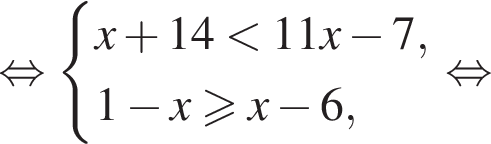
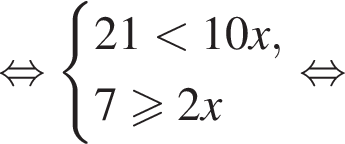
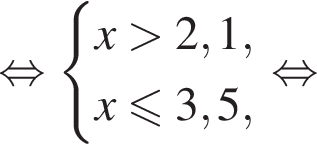
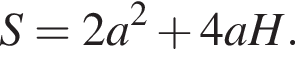
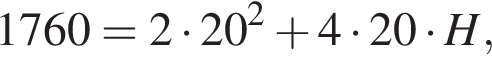
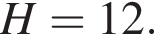
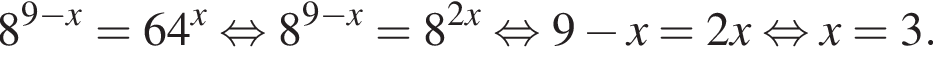
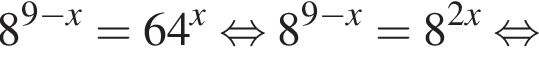
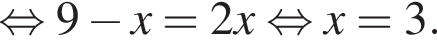
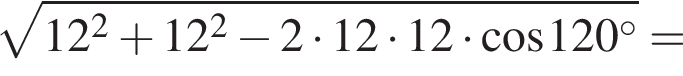
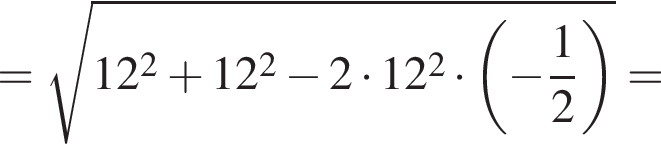
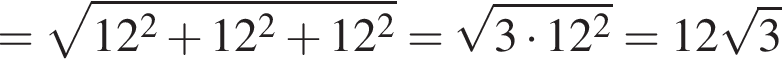
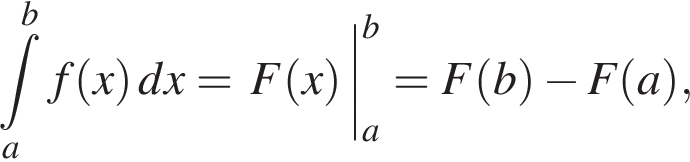
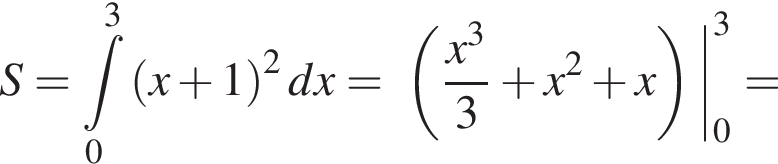
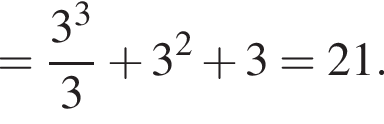
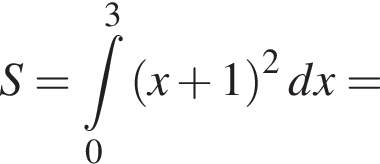
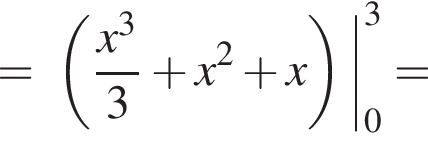
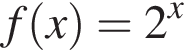не принимает отрицательных значений ни при каких значениях x, а значит, областью ее определения является промежуток 
Ответ — Б.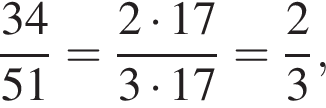
у остальных дробей числитель и знаменатель не имеют общих делителей, больших 1.
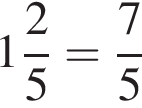будет дробь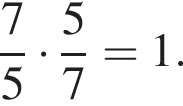 
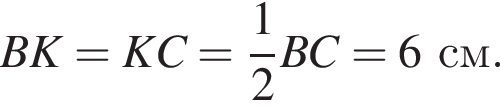
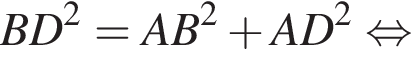
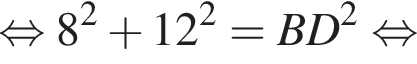
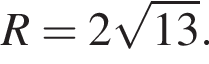поскольку 
Итак, 2 — А.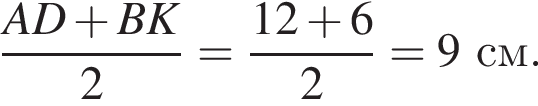
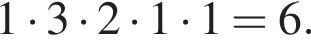
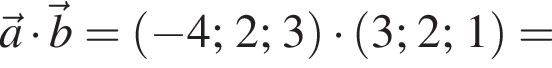
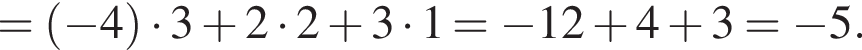
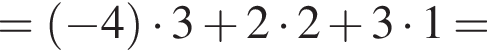
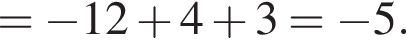
и 
Чтобы эти уравнения были равносильны между собой, их множества решений должны совпадать: либо 
либо оба уравнения не имеют решений. В первом случае 
и 
но второе значение параметра является посторонним, поскольку этому значению соответствуют два решения первого уравнения. Во втором случае — 
Следовательно, наибольшее целое значение равно 0.