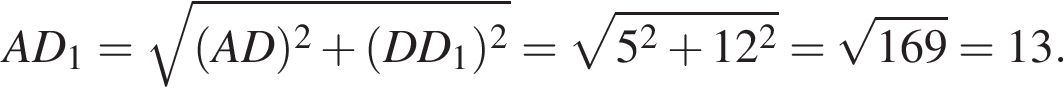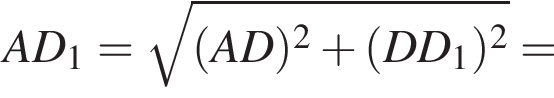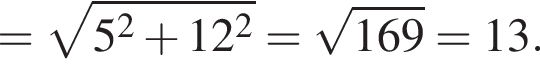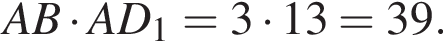У довільному експерименті симетричну монету кидають двічі. Знайдіть ймовірність того, що настане результат ОР (вперше випадає орел, вдруге - решка).
Для приготування фаршу взяли яловичину та свинину у співвідношенні 7:13. Який відсоток у фарші становить свинина?
На малюнку зображено трикутник ABC, у якому ∠ ACB = 38°, ∠ AMN = 109°. Використовуючи дані малюнка, знайдіть градусну міру кута BAC.
Розв’яжіть рівняння 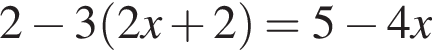 .
.
У правильній шестикутній призмі ABCDEFA1B1C1D1E1F всі ребра якої дорівнюють 8, знайдіть кут між прямими FA і D1E1. Відповідь дайте у градусах.
З точки А (6; 8) опущено перпендикуляр на вісь абсцис. Знайдіть довжину перпендикуляра.
Визначте число, 11% якого дорівнює 44.
Графік функції  паралельно перенесли вздовж осі x на 2 одиницi вправо. Графік якої з перерахованих функцій отримали?
паралельно перенесли вздовж осі x на 2 одиницi вправо. Графік якої з перерахованих функцій отримали?
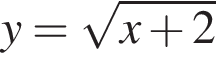
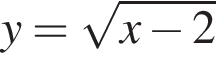



Скоротіть дріб 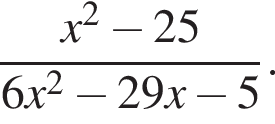
Які з наведених тверджень є правильними?
I. градусна міра розгорнутого кута дорівнює 180°.
II. У рівнобедреному трикутнику бісектриса, проведена до основи, є медіаною і висотою.
III. Площу рівностороннього трикутника можна знайти за формулою 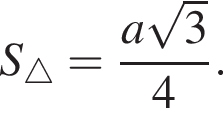
Знайдіть корінь рівняння 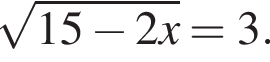
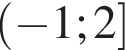
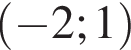
Укажіть похідну функції 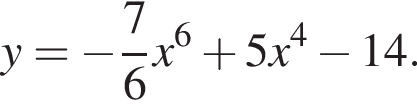
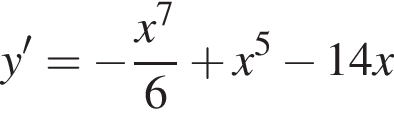
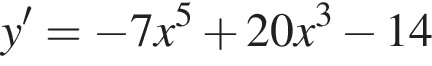
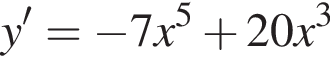
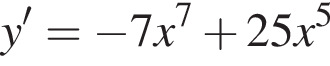
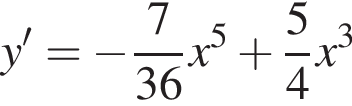
Розв'яжіть систему нерівностей: 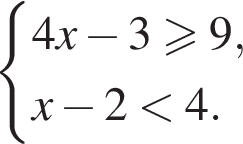


Розташуйте числа 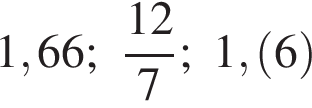 в порядку зростання.
в порядку зростання.
На рисунках (1−3) зображено графіки функцій, визначених на відрізку [−4; 4].
До кожного п очатку речення (1−3) доберіть його закінчення (А−Д) так, щоб утворилося правильне твердження.
1. Функція, графік якої зображ ено на рис. 1,
2. Функція, графік якої зображ ено на рис. 2,
3. Функція, графік якої зображ ено на рис. 3,
А рис. є непарною.
Б рис. набуває найбільшого значення, що дорівнює 4.
В рис. є парною.
Г рис. має три нулі.
Д рис. має дві точки локального екстремуму.
Установіть відповідність між виразом (1−4) та твердженням про його значення (А−Д) при а= 15.
1. ![]()
2. ![]()
3. 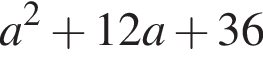
4. 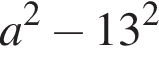
А менше за 20
Б є простим числом
В є парним
Г ділиться націло на 3
Д ділиться націло на 5
Установіть відповідність між геометричною фігурою (1—3) та радіусом кола (А—Д), вписаного в цю геометричну фігуру.
1. правильний трикутник, висота якого дорівнює ![]() (рис. 1)
(рис. 1)
2. ромб, висота якого дорівнює ![]() (рис. 2)
(рис. 2)
3. квадрат, діагональ якого дорівнює ![]() (рис. 3)
(рис. 3)
А ![]()
Б 1
В ![]()
Г ![]()
Д ![]()
Площини α i β паралельнi. Якi з наведених тверджень є правильними?
I. Iснує пряма, що лежить i в площинi α i в площини β.
II. Якщо пряма перпендикулярна до площини α, то вона перпендикулярна до площини β.
III. Якщо пряма лежить у площинi α, то вона паралельна будь-якiй прямiй у площинi β.
Виписані перші кілька членів геометричної прогресії: 17, 68, 272, … Знайдіть її четвертий член.
Відповідь: ,.
У прямокутному паралелепіпеді  відомі довжини ребер: AB = 3, AD = 5, AA1 = 12. Знайдіть площу перерізу паралелепіпеда площиною, що проходить через точки A, B і C1.
відомі довжини ребер: AB = 3, AD = 5, AA1 = 12. Знайдіть площу перерізу паралелепіпеда площиною, що проходить через точки A, B і C1.

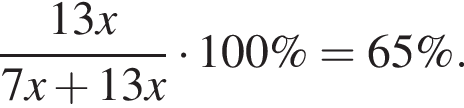
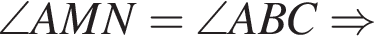
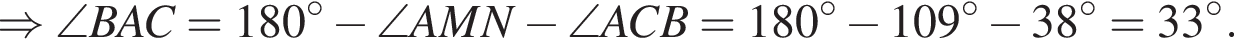
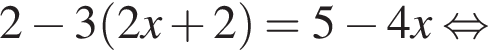
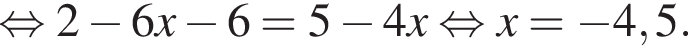
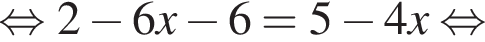
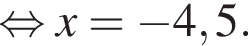
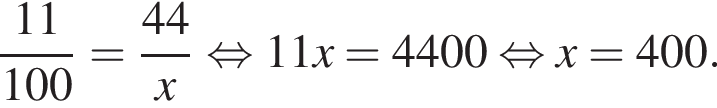
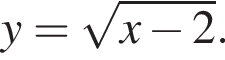
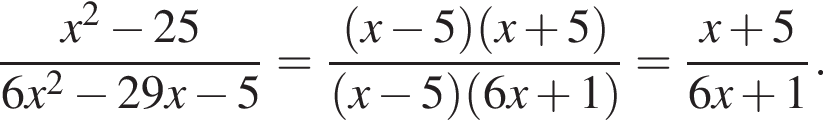
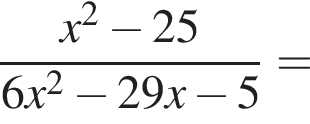
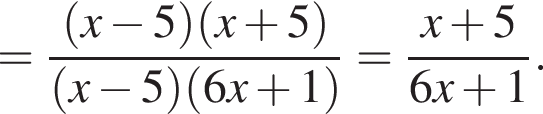
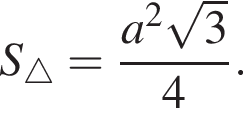
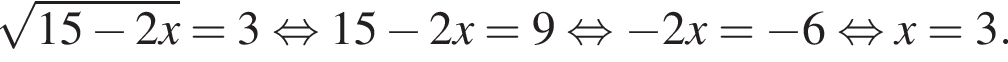


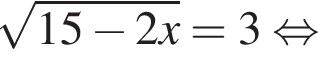

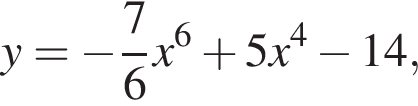 используя правило нахождения производной суммы функций:
используя правило нахождения производной суммы функций: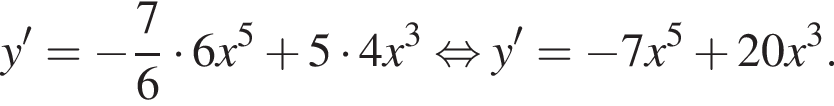
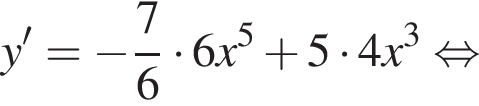
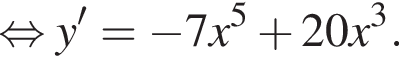
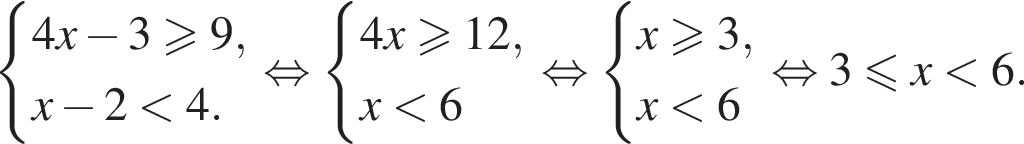
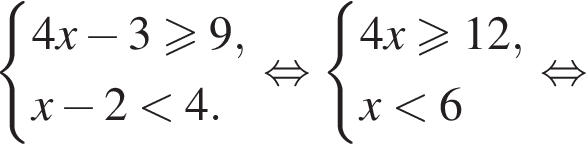
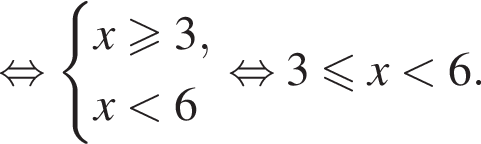
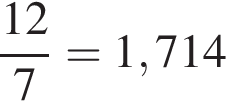 ;
; ;
; .
.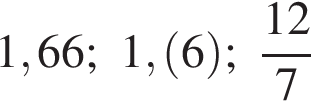 .
.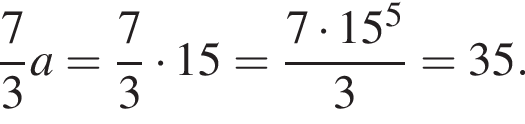
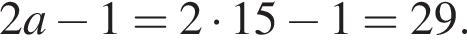 Полученное число является простым. Итак, 2 — Б.
Полученное число является простым. Итак, 2 — Б. 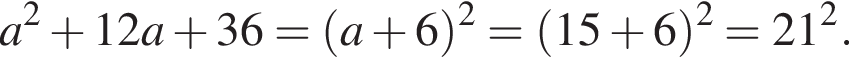
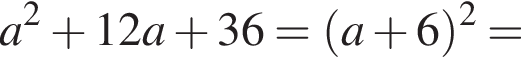
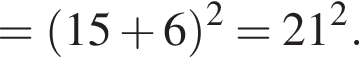
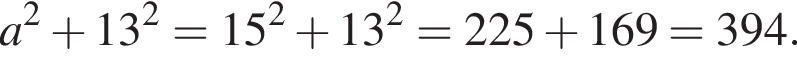
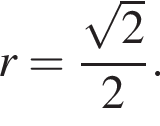 Получаем: 2 — Г.
Получаем: 2 — Г. 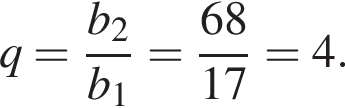

 — параллелограмм. Кроме того, ребро AB перпендикулярно граням
— параллелограмм. Кроме того, ребро AB перпендикулярно граням  и
и  Поэтому углы
Поэтому углы