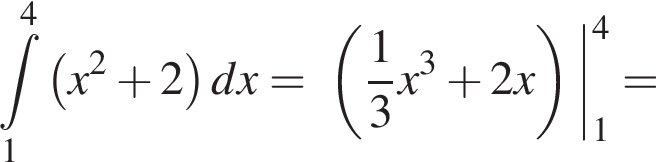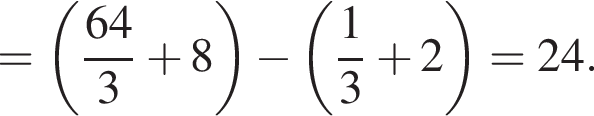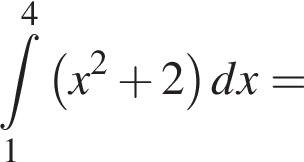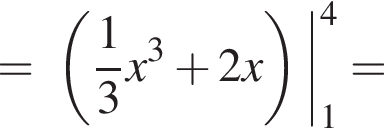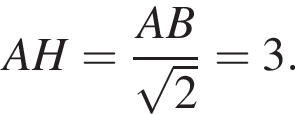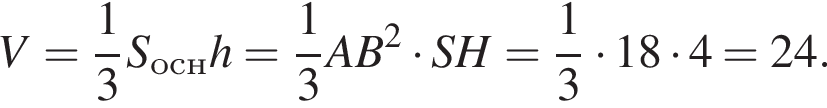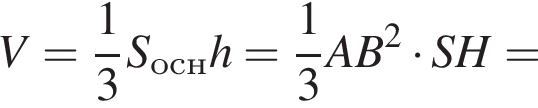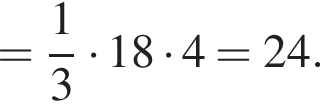Від пристані одночасно вирушають за течією річки катер (I) і проти течії річки моторний човен (II). На малюнку наведено графіки їхнього руху. Визначте швидкість течії річки (в км/год), якщо катер та моторний човен мають однакові власні швидкості.
Один кілограм яблук коштує на базарі від 9 грн до 12 грн, а один кілограм груш — від 19 грн до 25 грн. Оксана заплатила за куплені на базарі 2 кг яблук та 3 кг груш m гривень. Укажіть нерівність, що виконуватиметься для m.

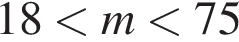
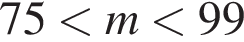
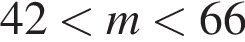
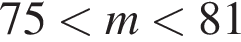
У куб з ребром 3 вписаний шар. Знайдіть обсяг цієї кулі, поділений на
![]()
Усі зображені на рисунку прямі лежать в одній площині, прямі m і n є паралельними. Визначте градусну міру кута а.
Найдите значение выражения 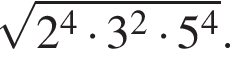
Розв’яжіть рівняння: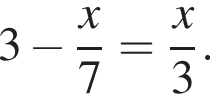
Знайдіть відстань від точки A з координатами (6; 8) до початку координат.
Графік функції  паралельно перенесли вздовж осі y на 3 одиниці вгору. Графік якої з перерахованих функцій отримали?
паралельно перенесли вздовж осі y на 3 одиниці вгору. Графік якої з перерахованих функцій отримали?
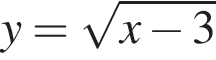


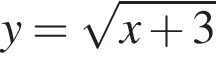

Які з наведених тверджень є правильними?
I. Діагоналі будь-якого ромба ділять його кути навпіл.
II. Діагоналі будь-якого чотирикутника точкою перетину діляться навпіл.
III. Діагоналі будь-якого квадрата перпендикулярні.
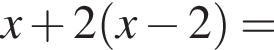
Вкажіть номер малюнка, на якому показано розв’язок системи нерівностей 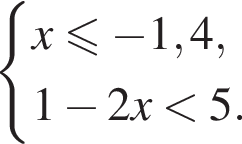
У прямокутному трикутнику гіпотенуза дорівнює 10, а один із гострих кутів дорівнює 45°. Знайдіть площу трикутника.
Дано геометричну прогресію ( bn ), знаменник якої дорівнює 2, а b1 = 16. Знайдіть b4.
Висота правильної чотирикутної піраміди дорівнює 24, апофема утворює з площиною основи піраміди кут 45°. Визначте довжину сторони основи цієї піраміди.
Укажіть кількість коренів рівняння 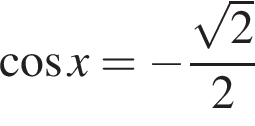 на відрізку
на відрізку 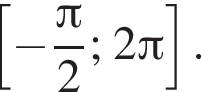
Доберіть до функції (1–3) ескіз її графіка (А–Д).
1. 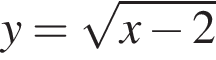
2. 
3. ![]()
Установіть відповідність між числовим виразом (1−4) та проміжком (А−Д), якому належить його значення.
1. 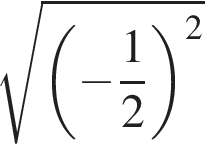
2. ![]()
3. 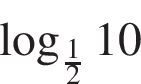
4. 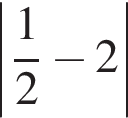
А 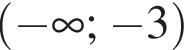
Б [−3; 0)
В [0; 1)
Г [1; 3)
Д 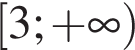
На рисунке изображена точка A на координатной плоскости. В зависимости от расположения точки B (1−3) найдите длину отрезка AB (А−Д).
1. Точка B симметрична точке A относительно оси Ox.
2. Точка B симметрична точке A относительно оси Oy.
3. Точка B симметрична точке A относительно начала координат.
А 3
Б 2
В ![]()
Г ![]()
Д 6
Обчисліть
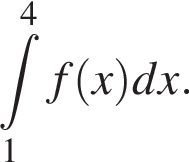 використавши зображений на рисунку графік квадратичної функції
використавши зображений на рисунку графік квадратичної функції 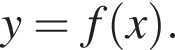
Відповідь: ,.
Перші 5 годин автомобіль їхав зі швидкістю 60 км/год, наступні 3 години зі швидкістю 100 км/год, а останні 4 години зі швидкістю 75 км/год. Знайдіть середню швидкість автомобіля протягом усього шляху.
Відповідь: ,.
У правильній чотирикутній піраміді SABCD з основою ABCD бічне ребро SA дорівнює 5, сторона основи дорівнює![]() Знайдіть обсяг піраміди.
Знайдіть обсяг піраміди.
Определите, при каких значениях параметра равносильны уравнения 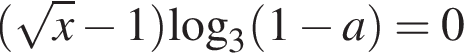 и
и 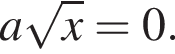
Відповідь: ,.

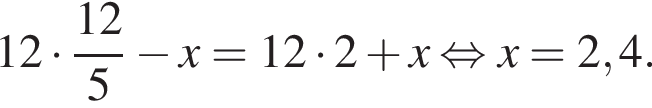
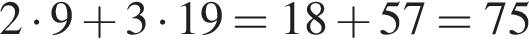 гривен, а если самые дорогие, то
гривен, а если самые дорогие, то  гривен. Значит
гривен. Значит 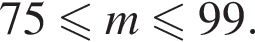
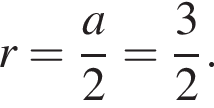 Тогда объем шара
Тогда объем шара 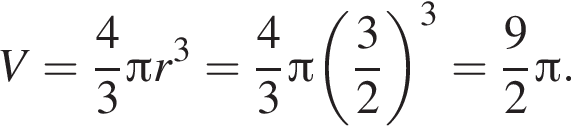
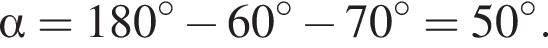
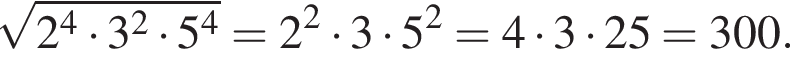
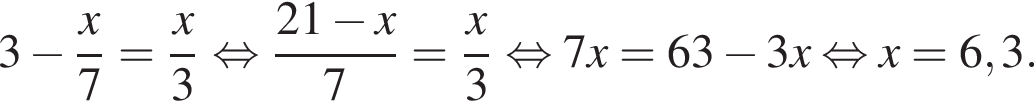
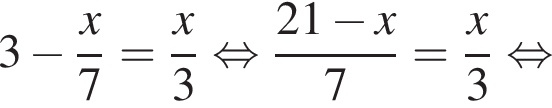
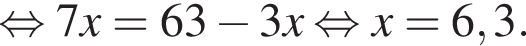
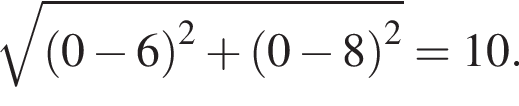


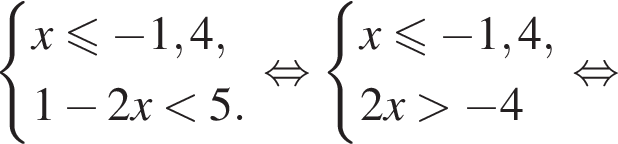
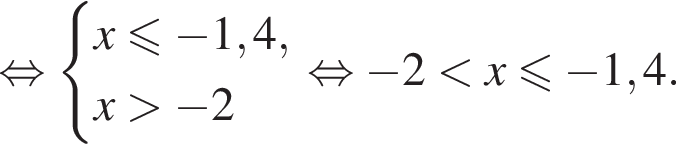
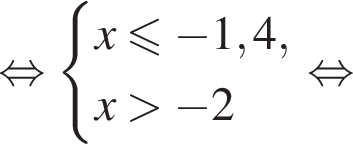
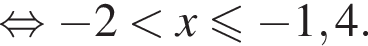
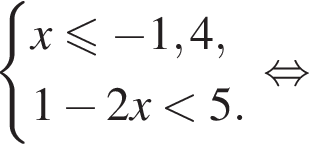
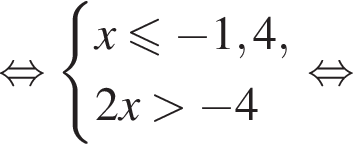
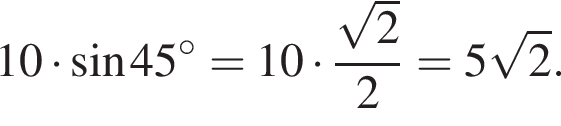
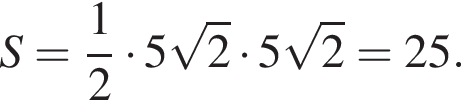
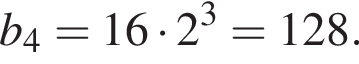
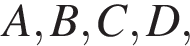 центр основания за O, середину AB за M. Тогда
центр основания за O, середину AB за M. Тогда 
 Значит
Значит  Итак, половина расстояния между сторонами AB и CD это 24, значит само расстояние (равное стороне BC квадрата ABCD) равно 48.
Итак, половина расстояния между сторонами AB и CD это 24, значит само расстояние (равное стороне BC квадрата ABCD) равно 48.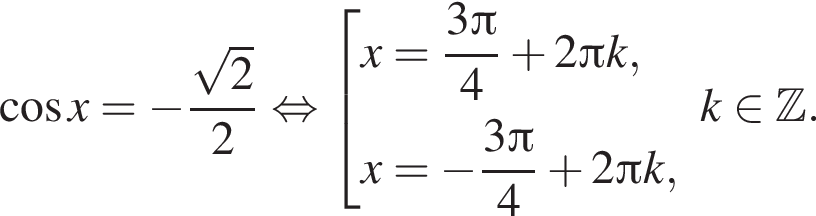
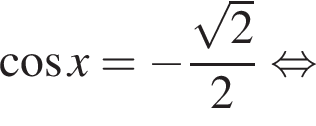
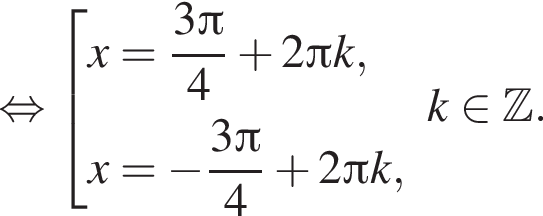
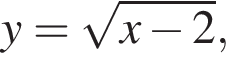 тогда
тогда  то есть на графике должна лежать точка (2; 0). Кроме того, при
то есть на графике должна лежать точка (2; 0). Кроме того, при 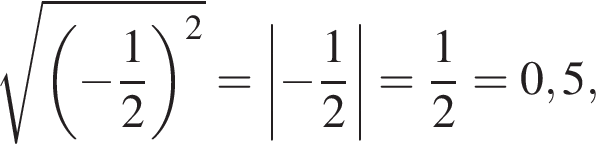
 Получаем, что 1 — B.
Получаем, что 1 — B.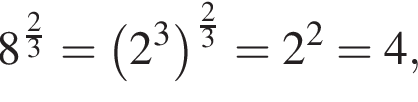 где
где 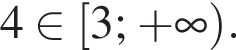 Итак, 2 — Д.
Итак, 2 — Д. 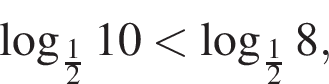 где
где 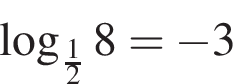 и
и 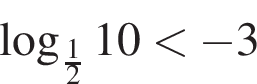 при
при 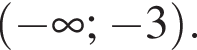 Следовательно, 3 — A.
Следовательно, 3 — A.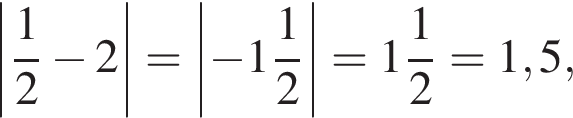
 Следовательно, 4 — Г.
Следовательно, 4 — Г.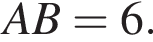
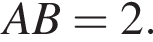
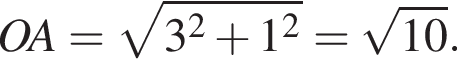
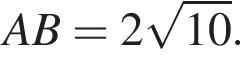
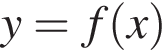 представляет собой параболу, ветви которой направлены вверх, вершина которой сдвинута на 2 единицы вверх. Следовательно, исходная функция
представляет собой параболу, ветви которой направлены вверх, вершина которой сдвинута на 2 единицы вверх. Следовательно, исходная функция  Вычислим интеграл:
Вычислим интеграл: