Установіть відповідність між виразом (1−3) і твердженням про його значення (А−Д), яке є правильним, якщо 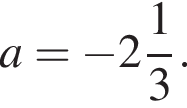
1. ![]()
2. ![]()
3. 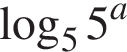
А більше від 5
Б належить проміжку (0; 1)
В є від’ємним числом
Г належить проміжку [1; 5)
Д дорівнює 0
Установіть відповідність між виразом (1−3) і твердженням про його значення (А−Д), яке є правильним, якщо 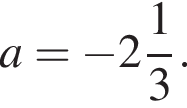
1. ![]()
2. ![]()
3. 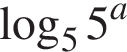
А більше від 5
Б належить проміжку (0; 1)
В є від’ємним числом
Г належить проміжку [1; 5)
Д дорівнює 0
Установіть відповідність між виразом (1−3) та твердженням про його значення (А—Д), яке є правильним, якщо 
1. ![]()
2. ![]()
3. 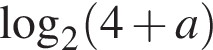
А дорівнює дробу ![]()
Б є від’ємним не цілим числом
В належить проміжку [0; 0,5]
Г є цілим числом
Д більше за 1
Установіть відповідність між виразом (1−3) та твердженням про його значення (А−Д) при а= 15.
1. ![]()
2. 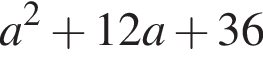
3. 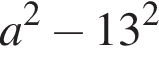
А менше за 20
Б є простим числом
В є парним
Г ділиться націло на 3
Д ділиться націло на 5
Нехай m і n — довільні дійсні числа, a — довільне додатне число, ![]() До кожного початку речення (1−3) доберіть його закінчення (А−Д) так, щоб утворилося правильне твердження.
До кожного початку речення (1−3) доберіть його закінчення (А−Д) так, щоб утворилося правильне твердження.
1. Якщо 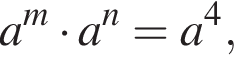 то
то
2. Якщо  то
то
3. Якщо 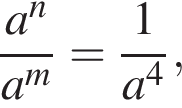 то
то
А 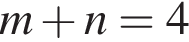
Б 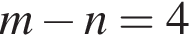
В 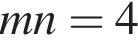
Г 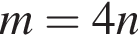
Д 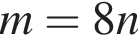
Установіть відповідність між твердженням про дріб (1−4) та дробом (А−Д), для якого це твердження є правильним.
1. є скоротним
2. є неправильним
3. є оберненим до дробу ![]()
А ![]()
Б ![]()
В ![]()
Г ![]()
Д ![]()
Установіть відповідність між запитанням (1−4) та правильною відповіддю на нього (А−Д).
1. Яке число є квадратом натурального числа?
2. Яке число є простим?
3. Яке число є дільником 8?
А 8
Б 16
В 17
Г 27
Д 56
До кожного початку речення (1−3) доберіть його закінчення (А−Д) так, щоб утворилося правильне твердження.
1. Сума чисел 32 і 18
2. Добуток чисел 32 і 18
3. Частка чисел 32 і 18
А є квадратом натурального числа
Б є числом, що ділиться наділо на 10
В є найменшим спільним кратним чисел 32 і 18
Г є раціональним числом, яке не є цілим
Д є дільником числа 84
Установіть відповідність між твердженням про дріб (1−3) та дробом, для якого це твердження є правильним (А−Д).
1. є правильним
2. належить проміжку (1; 1,5)
3. дорівнює значенню виразу 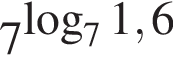
А ![]()
Б ![]()
В ![]()
Г ![]()
Д ![]()
Установіть відповідність між твердженням про дріб (1−3) та дробом, для якого це твердження є правильним (А-Д).
1. є сумою чисел ![]() та
та ![]()
2. дорівнює значенню виразу 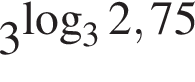
3. належить проміжку (2; 2,5)
А ![]()
Б ![]()
В ![]()
Г ![]()
Д ![]()
Узгодьте вираз (1–3) з твердженням (А–Д) про його значення, якщо а = 3.
1) a−1
2) a0
3) 
А) є раціональним числом, що не є цілим
Б) є натуральним числом
В) є цілим від’ємним числом
Г) є ірраціональним числом
Д) дорівнює 0