Спортивний магазин проводить акцію: «Будь-яка футболка за ціною 300 рублів. Купуючи дві футболки — знижка на другу 60%». Скільки рублів доведеться заплатити за покупку двох футболок?
Мотоцикліст першого дня подорожі проїхав 320 км, другого дня — 360 км, третього дня — 400 км, а четвертий — 208 км. Яку відстань у середньому за день проїжджав автомобіліст?
Що є основою правильної чотирикутної піраміди?
Обчисліть 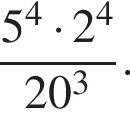
На малюнку зображені розгорнутий кут AOM та промені OB та OC. Відомо, що ∠ AOC = 144 °, ∠ BOM = 136 °. Знайдіть величину кута BOC.
Розв’яжіть рівняння: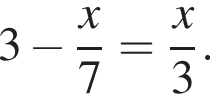
Графік функції, визначеної на проміжку [−5; 4], проходить через одну з наведених точок (див. рисунок). Укажіть цю точку.
Спростіть вираз 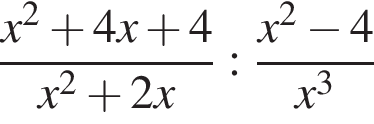 .
.
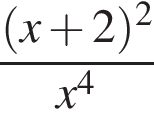
Які з наведених тверджень є правильними?
I. Якщо два кути одного трикутника дорівнюють двом кутам іншого трикутника, то такі трикутники подібні.
II. Якщо два кути трикутника рівні, то рівні також протилежні їм сторони.
III. Якщо діагоналі ромба дорівнюють 3 і 4, то його площа дорівнює 6.
Результат спрощення виразу 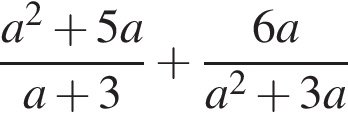 має вид:
має вид:
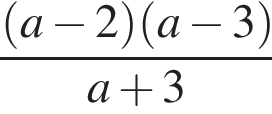
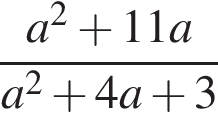
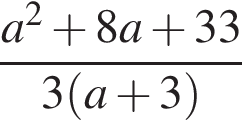
Розв'яжіть систему нерівностей 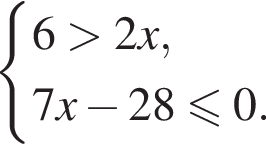
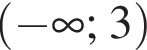
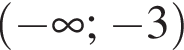
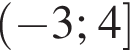
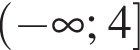
Знайдіть бічне ребро правильної чотирикутної призми, якщо сторона її основи дорівнює 20, а площа поверхні дорівнює 1760.
Знайдіть корінь рівняння: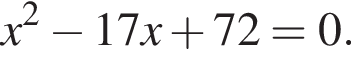
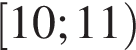
Довжина сторони ромба дорівнює 12 см. Визначте довжину більшої діагоналі цього ромба, якщо його тупий кут
На малюнку зображено графік деякої функції y = f(x) (два промені із загальною початковою точкою). Користуючись рисунком, обчисліть F(8) − F(2), де F(x) — одна з першорядних функцій f(x).
Увідповідніть функцію (1–3) та її властивість (А–Д).
1 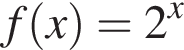
2 
3 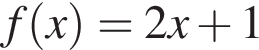
А функція непарна
Б областю значень функції є множина 
В областю визначення функції є проміжок 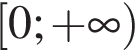
Г функція спадає на проміжку 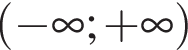
Д графік функції має лише дві точки перетину з осями координат
Нехай m і n — довільні дійсні числа, a — довільне додатне число, ![]() До кожного початку речення (1−3) доберіть його закінчення (А−Д) так, щоб утворилося правильне твердження.
До кожного початку речення (1−3) доберіть його закінчення (А−Д) так, щоб утворилося правильне твердження.
1. Якщо 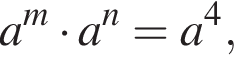 то
то
2. Якщо  то
то
3. Якщо 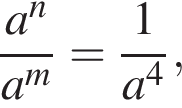 то
то
А 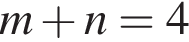
Б 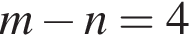
В 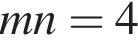
Г 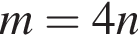
Д 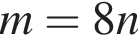
У прямокутник ABCD вписано рівнобедрений трикутник AKD так, як показано на рисунку. АD = 12 см, АК = 10 см. До кожного початку речення (1−3) доберіть його закінчення (А−Д) так, щоб утворилося правильне твердження.
1. Довжина сторони АВ дорівнює
2. Радіус кола, описаного навколо прямокутника АВСD, дорівнює
3. Довжина середньої лінії трапеції АВКD дорівнює
А ![]() см
см
Б 8 см
В 9 см
Г ![]() см
см
Д 4 см
Дана геометрична прогресія (bn), знаменник якої дорівнює 3, а 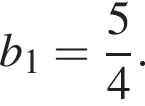 Знайдіть суму перших 6 членів прогресії.
Знайдіть суму перших 6 членів прогресії.
Відповідь: ,.
Блок реклами складається з 4 рекламних роликів: про шкоду куріння, про шкоду наркотиків, про шкоду алкоголю та велосипедне місто. Ролик про велосипедне місто заплановано показати двічі — першим та останнім, а решта трьох роликів — по одному разу. Скільки всього існує варіантів формування цього блоку реклами за вказаним порядком рекламних роликів?
Відповідь: ,.
Даны векторы 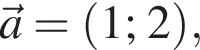
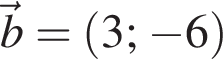 и
и 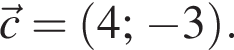 Найдите значение выражения
Найдите значение выражения 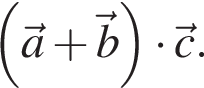
Відповідь: ,.
Визначте щонайменше целое значення а, за якого має корені рівняння 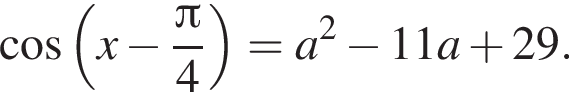
Відповідь: ,.

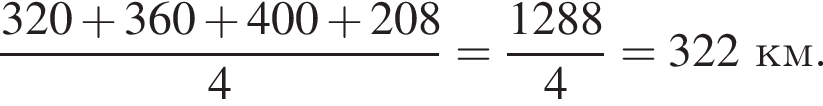
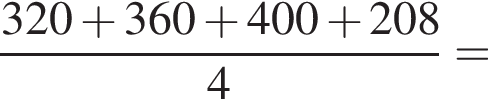
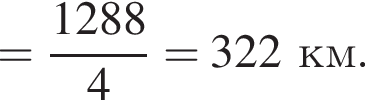
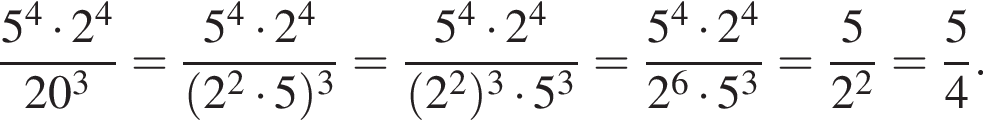
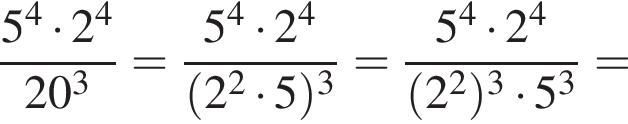
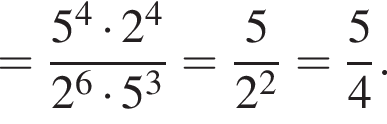
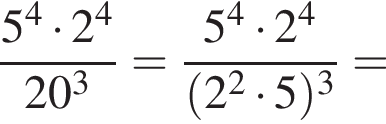
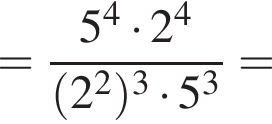
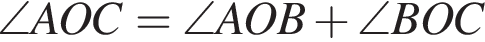 ,
, 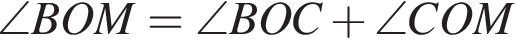 и
и  . Таким образом:
. Таким образом:
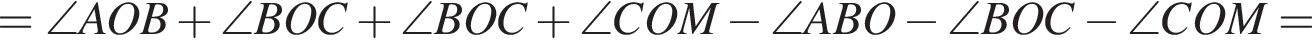
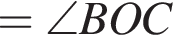
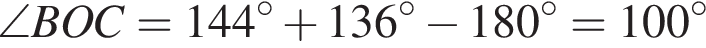 .
.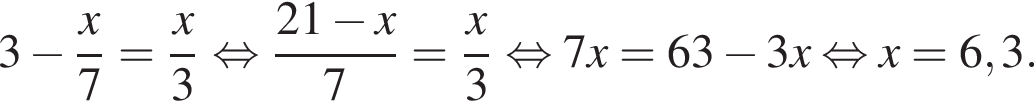
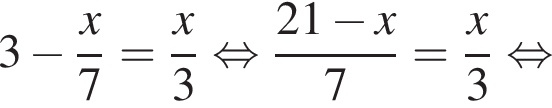
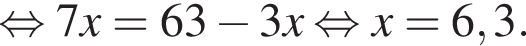
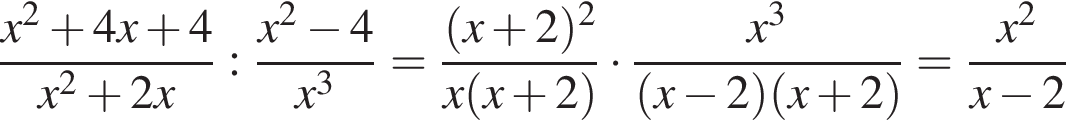
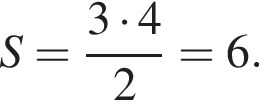
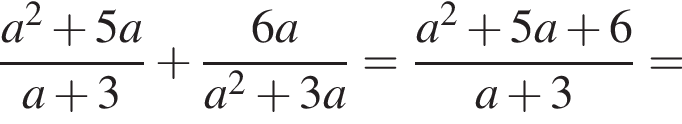
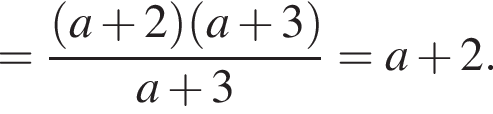
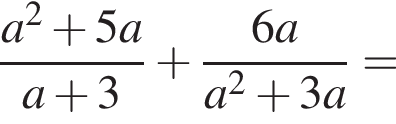
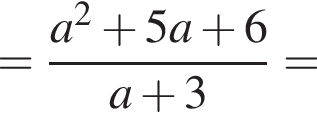
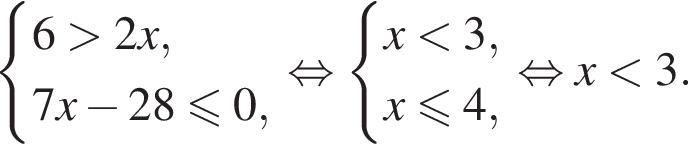
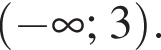
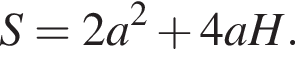
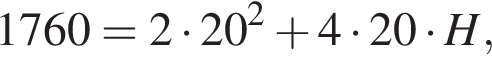
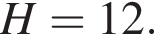
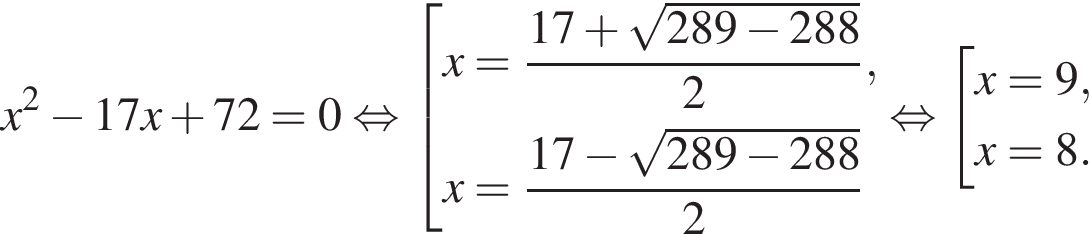
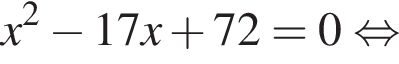
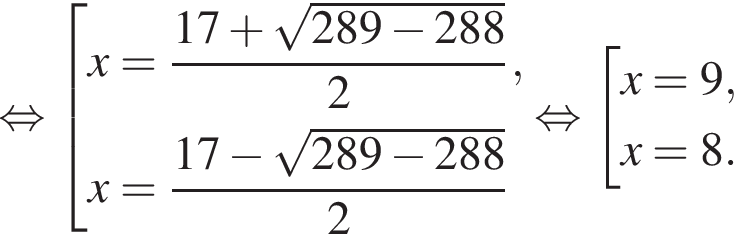
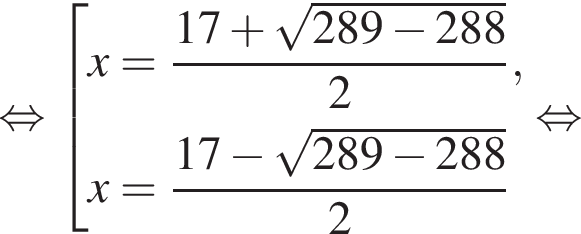
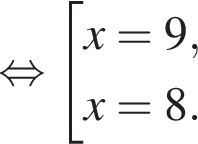
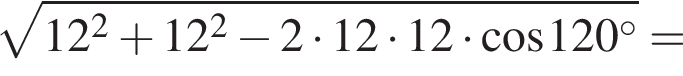
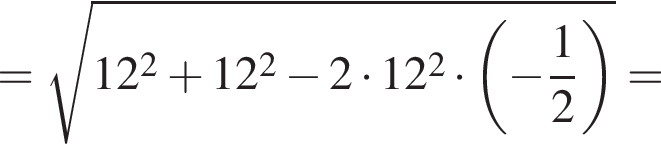
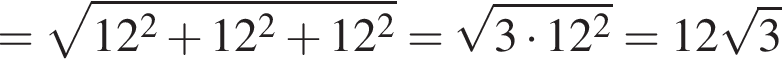
 Поэтому
Поэтому 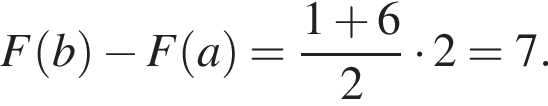
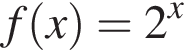 не принимает отрицательных значений ни при каких значениях x, а значит, областью ее определения является промежуток
не принимает отрицательных значений ни при каких значениях x, а значит, областью ее определения является промежуток  Ответ — Б.
Ответ — Б.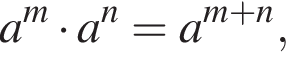 поэтому если
поэтому если 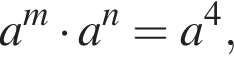 то
то 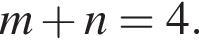
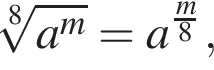
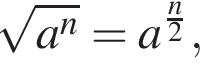 поэтому если
поэтому если  то
то 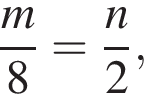 откуда
откуда 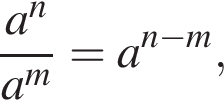 поэтому если
поэтому если 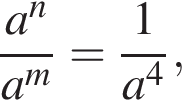 то
то 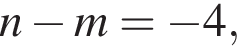
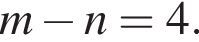
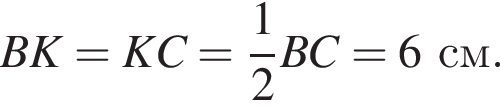


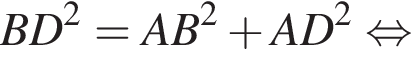
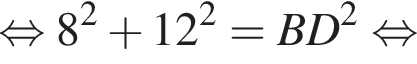
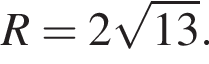 Итак, 2 — А.
Итак, 2 — А.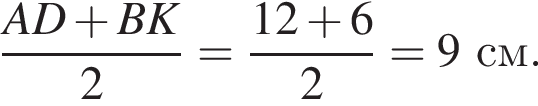
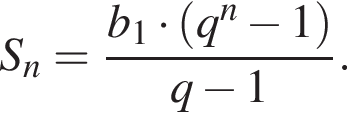
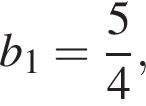
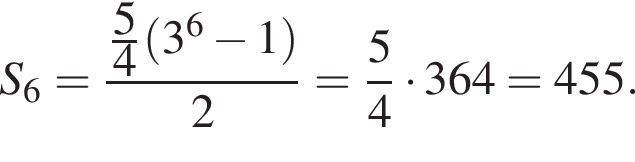
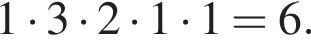
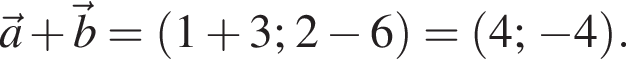
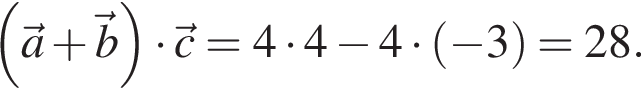
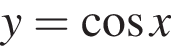 задается промежутком [−1; 1]. Найдем значения a, при которых уравнение
задается промежутком [−1; 1]. Найдем значения a, при которых уравнение 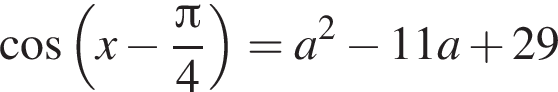 имеет решения:
имеет решения: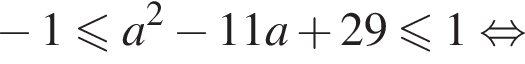
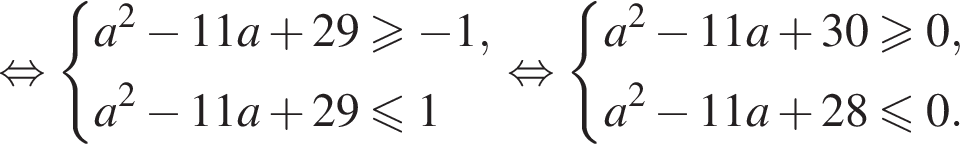
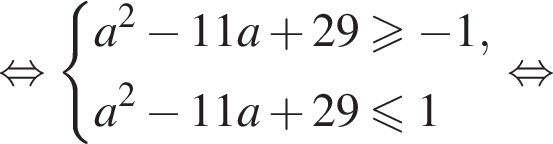
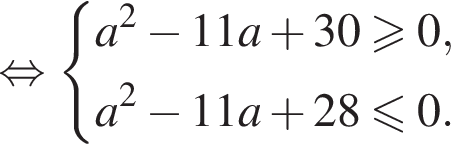
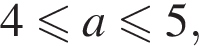
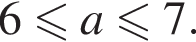 Таким образом, наименьшее целое значение a, при котором уравнение
Таким образом, наименьшее целое значение a, при котором уравнение