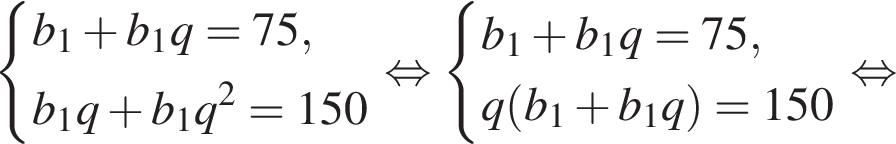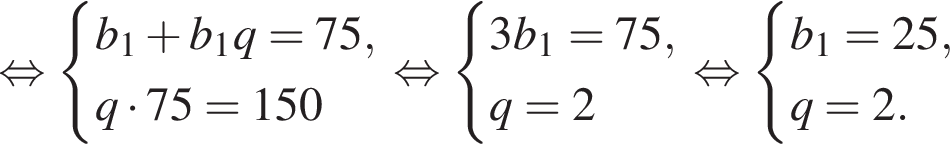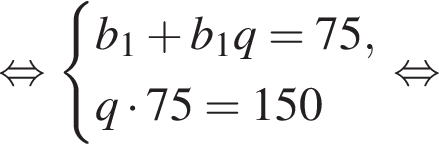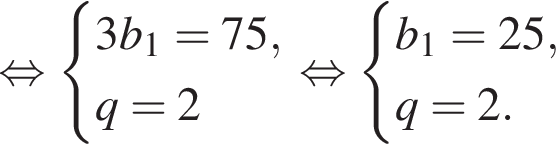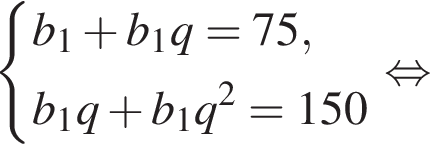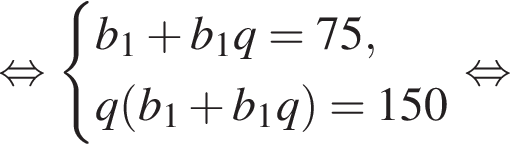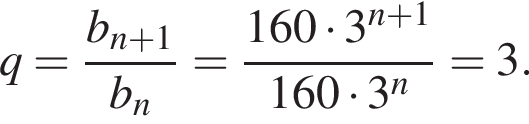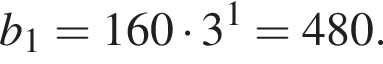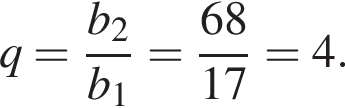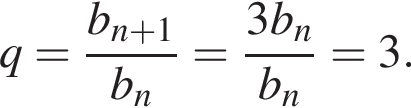Оочисліть другий член b2 геометричної прогресії (bn), якщо  та
та 
Дано геометричну прогресію ( bn ), знаменник якої дорівнює 2, а b1 = 16. Знайдіть b4.
Добуток другого та четвертого членів геометричної прогресії дорівнює 36. Усі члени цієї прогресії є додатними. Визначте третій член цієї прогресії.
У геометричній прогресії![]() відомо що
відомо що 
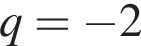 . Знайти п’ятий член цієї прогресії.
. Знайти п’ятий член цієї прогресії.
Геометрична прогресія ![]() задана формулою
задана формулою  Вкажіть четвертий член цієї прогресії.
Вкажіть четвертий член цієї прогресії.
У геометричній прогресії сума першого та другого членів дорівнює 75, а сума другого та третього членів дорівнює 150. Найдите первый член этой прогрессии.
Геометрична прогресія задана умовою 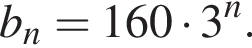 Найдите первый член этой прогрессии.
Найдите первый член этой прогрессии.
Виписані перші кілька членів геометричної прогресії: 17, 68, 272, … Знайдіть її четвертий член.
Геометрична прогресія задана умовою b1 = −7, bn + 1 = 3 bn. Найдите знаменатель геометрической прогрессии.

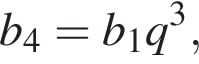 откуда
откуда 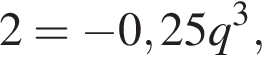
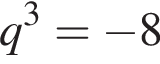 и
и 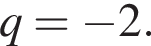 Значит,
Значит, 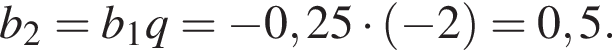
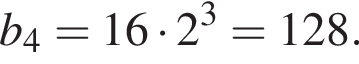
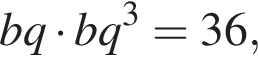 откуда
откуда 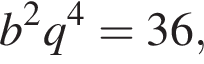
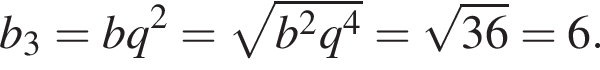
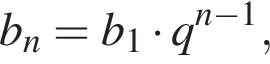 имеем:
имеем: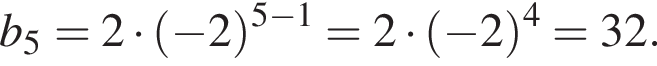
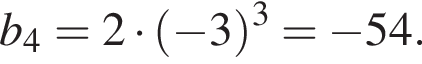
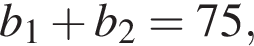
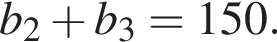 Запишем эти равенства в виде системы уравнений на первый член и знаменатель прогрессии и решим эту систему:
Запишем эти равенства в виде системы уравнений на первый член и знаменатель прогрессии и решим эту систему: