СКЛАДУ НМТ — математика

Задания

Тип 22 № 2259 Добавить в вариант

Источник: НМТ 2023 року з математики — демонстраційний варіант

Классификатор алгебры: Уравнения с параметром

Задачi з параметром. Завдання для підготовки

Визначте найменше ціле значення a, за якого один із коренів рівняння

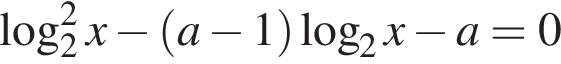
$логарифм по основанию 2 в квадрате x минус левая круглая скобка a минус 1 правая круглая скобка логарифм по основанию 2 x минус a = 0$

належить проміжку (30; 100).

Відповідь: ,.

Решение. Пусть 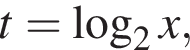$t= логарифм по основанию 2 x,$ тогда исходное уравнение записывается в виде

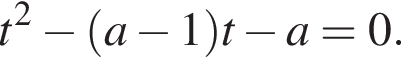
$t в квадрате минус левая круглая скобка a минус 1 правая круглая скобка t минус a=0.$

Полученное уравнение является квадратным относительно параметра, вычислим дискриминант уравнения:

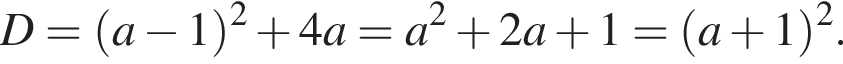
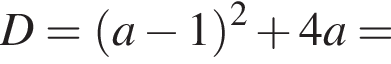
$D= левая круглая скобка a минус 1 правая круглая скобка в квадрате плюс 4a=a в квадрате плюс 2a плюс 1= левая круглая скобка a плюс 1 правая круглая скобка в квадрате .$ $D= левая круглая скобка a минус 1 правая круглая скобка в квадрате плюс 4a=$
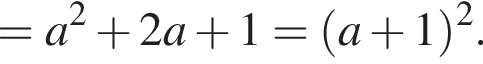
$=a в квадрате плюс 2a плюс 1= левая круглая скобка a плюс 1 правая круглая скобка в квадрате .$

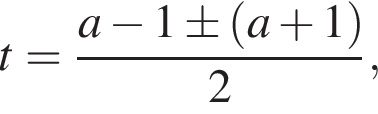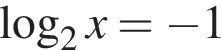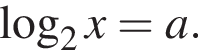Тогда $t= дробь: числитель: a минус 1\pm левая круглая скобка a плюс 1 правая круглая скобка , знаменатель: 2 конец дроби ,$ откуда $t= минус 1$ или $t=a,$ то есть $логарифм по основанию 2 x= минус 1$ или $логарифм по основанию 2 x=a.$ Из первого уравнения 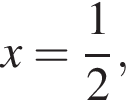$x = дробь: числитель: 1, знаменатель: 2 конец дроби ,$ этот корень не лежит в интервале (30; 100). Из второго уравнения 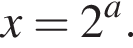$x=2 в степени a .$ Найдем наименьшее целое значение a, при котором корень этого уравнения принадлежит интервалу (30; 100):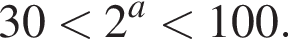

$30 меньше 2 в степени a меньше 100.$

Полученному неравенству удовлетворяют целые числа 5 и 6. Наименьшее из них равно 5.

Ответ: 5.

Примечание.

Искать корни квадратного уравнения удобно по теореме, обратной теореме Виета. Например, для уравнения

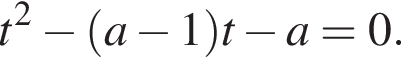
$t в квадрате минус левая круглая скобка a минус 1 правая круглая скобка t минус a=0.$

можно заметить, что сумма корней равна $a минус 1,$ а произведение равно –a. Ясно, что это числа $t=a$ и $t= минус 1.$

Ответ: 5

2259

Источник: НМТ 2023 року з математики — демонстраційний варіант

Классификатор алгебры: Уравнения с параметром

Ключ

№ п/п	№ задания	Ответ
1	2259	5